DSP Blockset

Cholesky Factorization

Factor a square Hermitian positive definite matrix into triangular components.

Library

Math Functions / Matrices and Linear Algebra / Matrix Factorizations

Description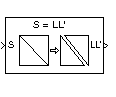

The Cholesky Factorization block uniquely factors the square Hermitian positive definite input matrix S as

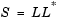
where L is a lower triangular square matrix with positive diagonal elements and L^* is the Hermitian (complex conjugate) transpose of L. The block outputs a matrix with lower triangle elements from L and upper triangle elements from L^*. The output is always sample-based.

Block Output Composed of L and L*

Input Requirements for Valid Output

The block output is valid only if its input has the following characteristics:

Note ·   Hermitian -- The block does not check whether the input is Hermitian; it uses only the diagonal and upper triangle of the input to compute the output.

• Real-valued diagonal entries -- The block disregards any imaginary component of the input's diagonal entries.
• Positive definite -- Set the block to notify you when the input is not positive definite as described in Response to Non-Positive Definite Input.

Response to Non-Positive Definite Input

To generate a valid output, the block algorithm requires a positive definite input (see Input Requirements for Valid Output). Set the Non-positive definite input parameter to determine how the block responds to a non-positive definite input:

• Ignore -- Proceed with the computation and do not issue an alert. The output is not a valid factorization. A partial factorization will be present in the upper left corner of the output.
• Warning -- Display a warning message in the MATLAB command window, and continue the simulation. The output is not a valid factorization. A partial factorization will be present in the upper left corner of the output.
• Error -- Display an error dialog and terminate the simulation.

Performance Comparisons with Other Blocks

Note that L and L^* share the same diagonal in the output matrix. Cholesky factorization requires half the computation of Gaussian elimination (LU decomposition), and is always stable.

Dialog Box

Non-positive definite input

Response to non-positive definite matrix inputs: Ignore, Warning, or Error. See Response to Non-Positive Definite Input. Tunable.

References

Golub, G. H., and C. F. Van Loan. Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

Supported Data Types

• Double-precision floating point
• Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Autocorrelation LPC	DSP Blockset
Cholesky Inverse	DSP Blockset
Cholesky Solver	DSP Blockset
LDL Factorization	DSP Blockset
LU Factorization	DSP Blockset
QR Factorization	DSP Blockset
chol	MATLAB

See Factoring Matrices for related information. Also see Matrix Factorizations for a list of all the blocks in the Matrix Factorizations library.

Chirp

Cholesky Inverse