

| DSP Blockset |   |
Solve the equation SX=B for X when S is a square Hermitian positive definite matrix.
Library
Math Functions / Matrices and Linear Algebra / Linear System Solvers
Description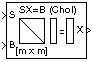
The Cholesky Solver block solves the linear system SX=B by applying Cholesky factorization to input matrix at the S port, which must be square (M-by-M) and Hermitian positive definite. Only the diagonal and upper triangle of the matrix are used, and any imaginary component of the diagonal entries is disregarded. The input to the B port is the right-hand side M-by-N matrix, B. The output is the unique solution of the equations, M-by-N matrix X, and is always sample-based.
When the input is not positive definite, the block reacts with the behavior specified by the Non-positive definite input parameter. The following options are available:
A length-M vector input for right-hand side B is treated as an M-by-1 matrix.
Algorithm
Cholesky factorization uniquely factors the Hermitian positive definite input matrix S as
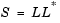
where L is a lower triangular square matrix with positive diagonal elements.
The equation SX=B then becomes
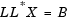
which is solved for X by making the substitution Y = L*X, and solving the following two triangular systems by forward and backward substitution, respectively.
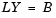
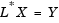
Dialog Box
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Autocorrelation LPC |
DSP Blockset |
| Cholesky Factorization |
DSP Blockset |
| Cholesky Inverse |
DSP Blockset |
| LDL Solver |
DSP Blockset |
| LU Solver |
DSP Blockset |
| QR Solver |
DSP Blockset |
chol |
MATLAB |
See Solving Linear Systems for related information. Also see Linear System Solvers for a list of all the blocks in the Linear System Solvers library.
 | Cholesky Inverse | Complex Cepstrum |  |