

| DSP Blockset |   |
Factor a rectangular matrix into unitary and upper triangular components.
Library
Math Functions / Matrices and Linear Algebra / Matrix Factorizations
Description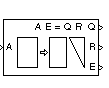
The QR Factorization block uses modified Gram-Schmidt iteration to factor a column permutation of the M-by-N input matrix A as
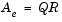
where Q is an M-by-min(M,N) unitary matrix, and R is a min(M,N)-by-N upper-triangular matrix. A length-M vector input is treated as an M-by-1 matrix, and is always sample-based.
The column-pivoted matrix Ae contains the columns of A permuted as indicated by the contents of length-N permutation vector E.
The block selects a column permutation vector E, which ensures that the diagonal elements of matrix R are arranged in order of decreasing magnitude.
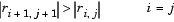
QR factorization is an important tool for solving linear systems of equations because of good error propagation properties and the invertability of unitary matrices.
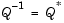
Unlike LU and Cholesky factorizations, the matrix A does not need to be square for QR factorization. Note, however, that QR factorization requires twice as many operations as Gaussian elimination.
Example
A sample factorization is shown below. The input to the block is matrix A, which is permuted according to vector E to produce matrix Ae. Matrix Ae is factored to produce the Q and R output matrices.
Dialog Box
References
Golub, G. H., and C. F. Van Loan. Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Cholesky Factorization |
DSP Blockset |
| LU Factorization |
DSP Blockset |
| QR Solver |
DSP Blockset |
| Singular Value Decomposition |
DSP Blockset |
qr |
MATLAB |
See Factoring Matrices for related information. Also see Matrix Factorizations for a list of all the blocks in the Matrix Factorizations library.
 | Pseudoinverse | QR Solver |  |