DSP Blockset

Factoring Matrices

The Matrix Factorizations library provides the following blocks for factoring various kinds of matrices:

• Cholesky Factorization
• LDL Factorization
• LU Factorization
• QR Factorization
• Singular Value Decomposition

Some of the blocks offer particular strengths for certain classes of problems. For example, the Cholesky Factorization block is particularly suited to factoring a Hermitian positive definite matrix into triangular components, whereas the QR Factorization is particularly suited to factoring a rectangular matrix into unitary and upper triangular components.

Example: LU Factorization

In the model below, the LU Factorization block factors a matrix A_p into upper and lower triangular submatrices U and L, where A_p is row equivalent to input matrix A, where

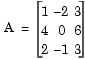
To build the model, in the DSP Constant block, set the Constant value parameter to [1 -2 3;4 0 6;2 -1 3].

The lower output of the LU Factorization, P, is the permutation index vector, which indicates that the factored matrix A_p is generated from A by interchanging the first and second rows.

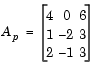
The upper output of the LU Factorization, LU, is a composite matrix containing the two submatrix factors, U and L, whose product LU is equal to A_p.

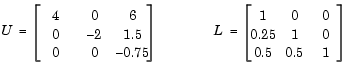
You can check that LU = A_p with the Matrix Multiply block, as shown in the model below.

Solving Linear Systems

Inverting Matrices