

| DSP Blockset |   |
Solve the equation UX=B for X when U is an upper triangular matrix.
Library
Math Functions / Matrices and Linear Algebra / Linear System Solvers
Description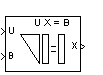
The Backward Substitution block solves the linear system UX=B by simple backward substitution of variables, where U is the upper triangular M-by-M matrix input to the U port, and B is the M-by-N matrix input to the B port. The output is the solution of the equations, the M-by-N matrix X, and is always sample-based. The block does not check the rank of the inputs.
The block uses only the elements in the upper triangle of input U; the lower elements are ignored. When Force input to be unit-upper triangular is selected, the block replaces the elements on the diagonal of U with ones. This is useful when matrix U is the result of another operation, such as an LDL decomposition, that uses the diagonal elements to represent the D matrix.
A length-M vector input at port B is treated as an M-by-1 matrix.
Dialog Box
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Cholesky Solver |
DSP Blockset |
| Forward Substitution |
DSP Blockset |
| LDL Solver |
DSP Blockset |
| Levinson-Durbin |
DSP Blockset |
| LU Solver |
DSP Blockset |
| QR Solver |
DSP Blockset |
See Solving Linear Systems for related information. Also see Linear System Solvers for a list of all the blocks in the Linear System Solvers library.
 | Autocorrelation LPC | Buffer |  |