QR Solver (DSP Blockset)

Find a minimum-norm-residual solution to the equation AX=B.

Library

Math Functions / Matrices and Linear Algebra / Linear System Solvers

Description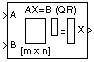

The QR Solver block solves the linear system AX=B, which can be overdetermined, underdetermined, or exactly determined. The system is solved by applying QR factorization to the M-by-N matrix, A, at the A port. The input to the B port is the right-hand-side M-by-L matrix, B. A length-M 1-D vector input at either port is treated as an M-by-1 matrix.

The output at the x port is the N-by-L matrix, X. X is always sample based, and is chosen to minimize the sum of the squares of the elements of B-AX. When B is a vector, this solution minimizes the vector 2-norm of the residual (B-AX is the residual). When B is a matrix, this solution minimizes the matrix Frobenius norm of the residual. In this case, the columns of X are the solutions to the L corresponding systems AX_k=B_k, where B_k is the kth column of B, and X_k is the kth column of X.

X is known as the minimum-norm-residual solution to AX=B. The minimum-norm-residual solution is unique for overdetermined and exactly determined linear systems, but it is not unique for underdetermined linear systems. Thus when the QR Solver is applied to an underdetermined system, the output X is chosen such that the number of nonzero entries in X is minimized.

Algorithm

QR factorization factors a column-permuted variant (A_e) of the M-by-N input matrix A as

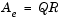
where Q is a M-by-min(M,N) unitary matrix, and R is a min(M,N)-by-N upper-triangular matrix.

The factored matrix is substituted for A_e in

and

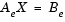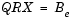
is solved for X by noting that Q^-1 = Q^* and substituting Y = Q^*B_e. This requires computing a matrix multiplication for Y and solving a triangular system for X.

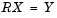
Dialog Box

Supported Data Types

Double-precision floating point
Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Levinson-Durbin
DSP Blockset

LDL Solver
DSP Blockset

LU Solver
DSP Blockset

QR Factorization
DSP Blockset

SVD Solver
DSP Blockset

Levinson-Durbin	DSP Blockset
LDL Solver	DSP Blockset
LU Solver	DSP Blockset
QR Factorization	DSP Blockset
SVD Solver	DSP Blockset

See Solving Linear Systems for related information. Also see Linear System Solvers for a list of all the blocks in the Linear System Solvers library.

QR Factorization Queue