

| DSP Blockset |   |
Solve the equation AX=B for X when A is a square matrix.
Library
Math Functions / Matrices and Linear Algebra / Linear System Solvers
Description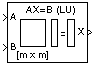
The LU Solver block solves the linear system AX=B by applying LU factorization to the M-by-M matrix at the A port. The input to the B port is the right-hand side M-by-N matrix, B. The output is the unique solution of the equations, M-by-N matrix X, and is always sample-based.
A length-M 1-D vector input for right-hand side B is treated as an M-by-1 matrix.
Algorithm
The LU algorithm factors a row-permuted variant (Ap) of the square input matrix A as
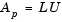
where L is a lower-triangular square matrix with unity diagonal elements, and U is an upper-triangular square matrix.
The matrix factors are substituted for Ap in
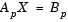
where Bp is the row-permuted variant of B, and the resulting equation
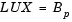
is solved for X by making the substitution Y = UX, and solving two triangular systems.
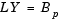
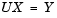
Dialog Box
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Autocorrelation LPC |
DSP Blockset |
| Cholesky Solver |
DSP Blockset |
| LDL Solver |
DSP Blockset |
| Levinson-Durbin |
DSP Blockset |
| LU Factorization |
DSP Blockset |
| LU Inverse |
DSP Blockset |
| QR Solver |
DSP Blockset |
See Solving Linear Systems for related information. Also see Linear System Solvers for a list of all the blocks in the Linear System Solvers library.
 | LU Inverse | Magnitude FFT |  |