DSP Blockset

Solving Linear Systems

The Linear System Solvers library provides the following blocks for solving the system of linear equations AX = B:

• Autocorrelation LPC
• Cholesky Solver
• Forward Substitution
• LDL Solver
• Levinson-Durbin
• LU Solver
• QR Solver
• SVD Solver

Some of the blocks offer particular strengths for certain classes of problems. For example, the Cholesky Solver block is particularly adapted for a square Hermitian positive definite matrix A, whereas the Backward Substitution block is particularly suited for an upper triangular matrix A.

Example: LU Solver

In the model below, the LU Solver block solves the equation Ax = b, where

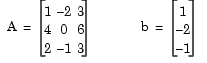
and finds x to be the vector [-2 0 1]'.

To build the model, set the following parameters:

• In the DSP Constant block, set Constant value = [1 -2 3;4 0 6;2 -1 3].
• In the DSP Constant1 block, set Constant value = [1 -2 -1]'.

You can verify the solution by using the Matrix Multiply block to perform the multiplication Ax, as shown in the model below.

Linear Algebra

Factoring Matrices