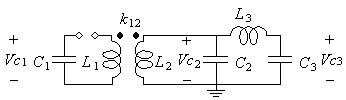
Below I describe what I have obtained working on the ideas that I found in the papers [1] and [2]. A set of formulas that allow, at least ideally (losses ignored, lumped model assumed as valid), the design of a perfect Tesla magnifier circuit, or triple resonance transformer, are presented.
A Tesla magnifier is a variation of the Tesla transformer where the resonator is separated from the secondary coil. The main objective of the modification is to obtain fast energy transfer without excessive voltage stress in the transformer. The magnifier is here modeled by the lumped circuit shown below:
The capacitor C1 is initially charged to a moderately high voltage, and when this voltage is high enough it discharges through the spark gap to the primary of the transformer L1L2, that has a coupling coefficient k12. The system enters then in an oscillatory transient, that eventually produces a very high voltage at the top terminal of the resonator coil, or third coil, L3.. C3 is usually a distributed capacitance, that represents the sum of the "self-capacitance" of L3 and the capacitance of a terminal placed above it. C2 represents the output capacitance of the transformer, added to other distributed and lumped capacitances at that point.
When C2 is negligible, this system behaves exactly as a normal Tesla coil [5], or double resonance transformer, with two oscillatory modes, as discussed below.
If C2 is significant, however, a third oscillatory mode appears, and the transient is more complex. Note that C2 may be very significant if the driver transformer has its windings at short distance. The ideal design would eventually put all the energy that was stored in C1 in C3 only, with zero voltages at C1 and C2, and zero currents at L1, L2, and L3 at that instant.
The problem is at first sight very complex, but it has a
closed form solution, that is described (with some errors in the
formulas that I had to figure out) in [1][2]. The nulling of the
currents when the energy transfer is complete leads to sets of
ideal relations among the three oscillation frequencies that
makes them to be ratios of integer numbers k: l: m, so that l =
k+1, k+3, k+5, ..., and m = l+1, l+3, l+5, ...
Ex: k:l:m = 1:2:3; 1:2:5; 2:3:4; 2:3:6; etc.
These three numbers define the "mode" of the operation.
Some extra conditions must be added to force the condition of
total energy transfer to C3. The details are in the
papers.
The design formulas, as functions of these three integers, are:
1) w2L1C1 = (2m2k2+(m2-l2)(l2-k2))/(2k2l2m2) 2) w2L2C2 = l2/(k2m2) 3) w2L3C3 = 1/l2 4) L2/L3 = ((l2-m2)(k2-l2))/(2*k2m2) 5) k122 = ((k2-l2)(l2-m2))/(k2(l2+m2)-l2(l2-m2))
The circuit oscillates simultaneously at the frequencies wk, wl, and wm rad/s. The complete energy transfer occurs after p/w seconds, at the "l"th peak (semicycle) of VC3.
As for every k:l:m there are 8 unknowns to be computed from 5 relations, 3 values are arbitrary. For example, w, C1 and C3, fixing the voltage amplification factor, that is (C1/C3)1/2, and the energy transfer time. The formulas allow the computation of the three inductances, C2, and k12. Once defined the geometry of the system, the self-capacitance of the third coil would be computed (by Medhurst's empirical formula [3], for example) and subtracted from the terminal capacitance, and an extra capacitor, distributed if possible (a toroidal terminal in L2) would be added in parallel with the transformer output capacitance and the input capacitance of L3 (approximately identical to its self-capacitance if the base of L3 is sufficiently far from the ground) to make C2.
Additional useful relations that can be obtained from the equations above are:
6) L1C1 = (L2+L3)C3 7) k122 = L2/(L2+L3) 8) C2/C3 = 2l4/((l2-m2)(k2-l2)) 9) L1C1(1-k122) = L3C3
A design can then be made without direct use of w:
L3 and C3 can be obtained from an
adequate resonator coil with a top terminal.
L2 can be obtained from the equation for L2/L3
(4) and the mode k:l:m.
L1 comes from a given C1 and the first
additional relation (6) above.
C2 comes from the relation for C2/C3
(8) and the mode.
k12 comes from the second (7) or from the fourth (9)
additional relation.
With these formulas, C2 can be left to be determined experimentally, as the distributed capacitances associated with the transformer and the base of L3 may be difficult to predict.
Observe that the fourth relation above says that the resonator L3C3 resonates at the same frequency of the primary system when C2 is short-circuited. (3) then says that both circuits, alone, resonate at the central frequency of the three where the whole circuit resonates.
When m is much greater than k and l, the circuit behaves as when C2=0, and the formulas still work correctly, with the special values of the coupling coefficient for optimal transfer obtained from the several combinations of k and l.
Optimum designs for a conventional Tesla coil can also be obtained, by adding L3 to L2 (forming L3'), and adjusting the coupling coefficient to k123 = k12(L2/(L2+L3))1/2. The resulting formulas are:
w2L1C1 = w2C3L3' = (k2+l2)/(2k2l2) k123 = (l2-k2)/(l2+k2)
Note that in this case the first formula serves only for the determination of "w". The oscillation frequencies of the resulting system are then wk and wl rad/s. The important relation is L1C1 = L3'C3.
Example of a magnifier (nothing specially optimized or realistic chosen):
Let k:l:m = 2:3:4, and let's fix L1, L3,
and w:
w=2p200000
(total energy transfer in 2.5 µs)
L1 = 0.1 mH
L3 = 20 mH
The remaining elements are then:
L2 = 5.47 mH
C1 = 896 pF
C2 = 16.28 pF
C3 = 3.52 pF
k12 = 0.463
A simulation of this circuit shows perfect transfer in 2.5 µs, and 159.5 kV in C3 for initial 10 kV in C1, corresponding exactly to the ideal factor of (896/3.52)1/2=15.95. All the other voltages and all the currents (not shown below) are zero at the peak of VC3.
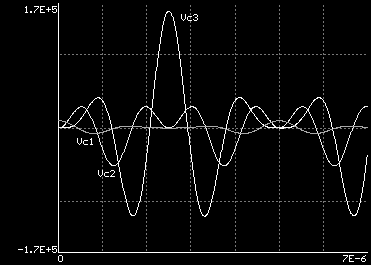
Voltage waveforms for the modes with klm=1:2:3, 1:2:5, 1:2:7, and 1:2:9, and for the modes with k:l:m=1:2:3, 2:3:4, 3:4:5, and 4:5:6. All the examples with C1=1 nF, C3=10 pF (for voltage amplification of 10 only), and w=2p200 krad/s.
Take also a look in my double resonance simulator TeslaSim, that allows experiments with Tesla coil circuits, and also inversion of Laplace transforms. The program MagSim, that designs systems based on the formulas presented here, and can generate Laplace transforms to be used in the TeslaSim program, is also available. See also the program Mrn6.
The theory initially developed in [1][2] can be generalized and extended to more complex configurations, with the help of some classical linear circuit theory. The papers [4][6] show the generalization to the case of "multiple resonance networks". See also [7], for a variant design technique, and [8], where it's shown that the initial energy can be in the first inductor instead of in the first capacitor. See also my pages about a transformerless Tesla coil, a capacitive transformer Tesla coil, a transformerless magnifier, a classical Tesla coil, and a Tesla magnifier, designed with help of the theory.
The paper [5] is an old reference about the theory of Tesla transformers. A partial translation of it to English is available.
References:
[1] F. M. Bieniosek, Review of Scientific Instruments 61 (6)
p. 1717, June 1990.
[2] F. M. Bieniosek, Proc. 6th IEEE Pulsed Power Conference, p.
700, 1987.
[3] R. G. Medhurst, "H. F. resistance and self-capacitance
of single-layer solenoids," Wireless Engineer, February
1947, pp. 35-43, continued in March
1947, pp. 80-92 (1).
[4] A. C. M. de Queiroz, "Synthesis of multiple resonance
networks," 2000 IEEE ISCAS, Geneva, Switzerland, May 2000,
Vol. V, pp. 413-416. Text (2).
[5] Drude, P. "Uber induktive Erregung zweier elektrischer
Schwingungskreise mit Anwendung auf Perioden und
Dampfungsmessung, Tesla transformatoren und drahtlose
Telegraphie," Annalen der Physik, pp. 512-561, vol. 13,
1904. Text (1).
[6] A. C. M. de Queiroz, "Multiple resonance networks,"
IEEE Transactions on Circuits and Systems I, Vol. 49, No. 2,
February 2002, pp. 240-244.
[7] A. C. M. de Queiroz, "A simple design technique for
multiple resonance networks," ICECS’2001, St. Julians,
Malta, September 2001, Vol. I, pp. 169-172. Text (2).
[8] A. C. M. de Queiroz, "Generalized Multiple Resonance
Networks, " 2002 IEEE ISCAS, Scottsdale, USA, May 2002, Vol
III, pp. 519-522. Text (2).
1) Djvu format.
2) PDF format. Copyrighted material by the IEEE.
Created: 6 May 2000
Last update: 8 October 2003
Developed and Maintained by Antonio Carlos M. de
Queiroz