Signal Processing Toolbox

xcorr

相互相関関数の推定

表示

c = xcorr(x,y)
c = xcorr(x)
c = xcorr(x,y,'option')
c = xcorr(x,'option')
c = xcorr(x,y,maxlags)
c = xcorr(x,maxlags)
c = xcorr(x,y,maxlags,'option')
c = xcorr(x,maxlags,'option')
[c,lags] = xcorr(...)

詳細

xcorrは、ランダムプロセスの相互相関列を推定します。自己相関は、特殊なケースとして扱われます。

真の相互相関列は、つぎのように表されます。

ここで、x_nとy_nは定常ランダムプロセスで、は、E {} は期待値演算子です。実際には、無限長のランダムプロセスの有限部分しか利用できないため、xcorrは、データ列を推定しなければなりません。

c = xcorr(x,y) は、相互相関列を長さ2N -1のベクトルに出力します。ここで、xとyは長さN のベクトルです。xとyが同じ長さでない場合、短いほうのベクトルにゼロを付加し、長いほうのベクトルと同じ長さにします。

デフォルトでは、xcorrは、正規化をせずに生データの相関を計算します。

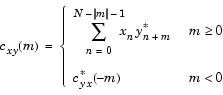
出力ベクトルcは、c(m) = c_xy(m-N), m=1, ..., 2N-1によって与えられる要素をもちます。

一般に、相関関数は、関数を正しく推定するために正規化を必要とします。

c = xcorr(x) は、ベクトルxの自己相関列です。xがN行P列の行列の場合、c = xcorr(x)は、P²列がxの列のすべての組合せに対する相互相関列を含む2N-1 行の行列を出力します。

c = xcorr(x,y,'option') は、スケーリングオプションを設定します。ここで、'option'には、つぎの文字列が設定できます。

• 'biased': 相互相関関数のバイアスのある推定

• 'unbiased': 相互相関関数の不偏(バイアスなし)推定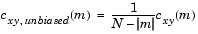

• 'coeff'：ゼロ遅れでの自己相関が、1.0になるように正規化します。
• none：スケーリングされていない生データの相互相関を使用(デフォルト)

バイアスのある推定と不偏推定の特性の詳細については、参考文献[1]を参照してください。

c = xcorr(x,'option') は、自己相関に対して、上の正規化オプションの一つを設定します。

c = xcorr(x,y,maxlags) は、ラグが[-maxlags:maxlags]の範囲について、相互相関列を計算し、出力c の長さは、2*maxlags+1になります。

c = xcorr(x,maxlags) は、ラグが[-maxlags:maxlags]の範囲について自己相関列を出力します。出力cは、長さ2*maxlags+1になります。xがN行P列の行列の場合、cはxの列に関するすべての組み合わせに対する自己相関列を含むP²列で、2*maxlags+1列の行列になります。

c = xcorr(x,y,maxlags,'option') は、相互相関に対して、ラグの最大数とスケーリングオプションを設定します。

c = xcorr(x,maxlags,'option') は、自己相関に対して、ラグの最大数とスケーリングオプションを設定します。

[c,lags] = xcorr(...) は、範囲[-maxlags:maxlags]で、推定した相関列cについて、ラグのインデックスベクトルを出力します。 maxlagsが設定されていないとき、lagsの範囲は、[-N+1:N-1]になります。

すべての場合、xcorrにより計算される相互相関、自己相関は、出力列の中央またはmaxlags+1行目にゼロラグのものを設定します(maxlagsが設定されていなければ、N番目の要素または列)。

例題

自己相関または相互相関をプロットするときには2番目の出力lagsが有効です。たとえば、つぎのステートメントを使って、平均がゼロのGauss性白色ノイズc_ww(m))の推定自己相関を -10 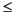m 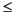10 に対して表示することができます。

ww = randn(1000,1);
[c_ww,lags] = xcorr(ww,10,'coeff');
stem(lags,c_ww)

xとyの入力引数を交換すると、出力される相関列が逆になります(そして、共役となります)。行ベクトルの場合、得られる列の左右が逆になり、列ベクトルの場合、上下が逆になります。つぎの例題では、この特性を示します(mat2str は、複素数のコンパクトな表示のために使用します)。

x = [1,2i,3]; y = [4,5,6];
[c1,lags] = xcorr(x,y);
c1 = mat2str(c1,2), lags

c1 =
    [12-i*8.9e-016 15-i*8 22-i*10 5-i*12 6+i*8.9e-016]

lags =
    -2    -1     0     1     2

c2 = conj(fliplr(xcorr(y,x)));
c2 = mat2str(c2,2)

c2 =
    [12-i*8.9e-016 15-i*8 22-i*10 5-i*12 6+i*8.9e-016]

入力引数xが行列の場合、出力される列は、行を抽出して、それを正方行列に再配列することにより、選択した行の遅れに対応する相互相関行列が作成されるように並べ替えます。たとえば、遅れゼロの相互相関は、つぎのステートメントにより取り出すことができます。

randn('seed',0)
X = randn(2,2);
[M,P] = size(X);
c = xcorr(X);
c0 = zeros(P); c0(:) = c(M,:)   % ゼロ遅れの行を抽出

c0 = 
    1.7500    0.3079
    0.3079    0.1293

上記の例で、ステートメントに置き換えると、MATLABの関数corrcoef が生成する相関係数の行列を計算することができます。

c = xcov(X,'coef')

関数xcovは、平均を除去してからxcorrを使います。

fftshiftを使って、遅れゼロに対応するものを中心に移動することができます。fftshiftは、データ列の前半と後半を交換します。

アルゴリズム

共分散および相関関数の推定の詳細については、参考文献[1]および[2]を参照してください。

参考

conv	コンボリューションおよび多項式乗算
corrcoef	相関係数行列
cov	共分散行列
xcorr2	2次元相互相関
xcov	相互共分散関数

参考文献

[1] Bendat, J.S., and A.G. Piersol, Random Data: Analysis and Measurement Procedures, John Wiley & Sons, New York, 1971, p. 332.

[2] Oppenheim, A.V., and R.W. Schafer, Digital Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1975, pp. 63-67, 746-747, 839-842.

vco

xcorr2