xcov (Signal Processing Toolbox)

相互共分散関数の推定

表示

v = xcov(x,y)
v = xcov(x)
v = xcov(x,'option')
[c,lags] = xcov(x,y,maxlags)
[c,lags] = xcov(x,maxlags)
[c,lags] = xcov(x,y,maxlags,'option')

詳細

xcovは、ランダムプロセスの相互共分散列を推定します。自己共分散は、特殊なケースです。

真の相互共分散列は平均除去相互相関列であり、つぎのように表されます。

ここで、m_xとm_y は2つの定常ランダムプロセスの平均値、E{} は期待定値演算子です。実際には、無限長のランダムプロセスの有限部分しか利用できないため、xcovは、データ列を推定しなければなりません。

v = xcov(x,y) は、相互共分散列を長さ2N-1のベクトルに出力します。ここで、xとyは、長さNのベクトルです。

v = xcov(x) は、ベクトルxの自己共分散列です。xがN行P 列の配列の場合、v = xcov(X)は、そのP²列がXの列のすべての組合せに対する相互共分散列を含む2N-1行の配列を出力します。

デフォルトでは、xcovは正規化をせず、生データの共分散を計算します。長さNのベクトルの場合には、つぎのようになります。

出力ベクトルcは、c(m) = c_xy(m-N), m=1,...,2N-1によって与えられる要素をもちます。

共分散関数は、関数を正しく推定するために正規化を必要とします。

v = xcov(x,'option') は、スケーリングオプションを設定します。ここで、optionには、つぎの文字列が設定できます。

biased：相互共分散関数のバイアス付き推定

unbiased：相互共分散関数の不偏推定

coeff：ゼロ遅れでの自己共分散が、1.0となるように正規化します。

none：スケーリングを適用しない相互共分散を使用(デフォルト)

相関/共分散のバイアスのある推定および不偏推定の特性の詳細については、参考文献[1]を参照してください。

[c,lags] = xcov(x,y,maxlags) は、xとyが長さmのベクトルとすると、[c,lags] = xcov(x,y,maxlags) は、相互共分散列を長さ2*maxlags+1のベクトルcに出力します。lagsは、cを推定した遅れインデックスのベクトル、すなわち[-maxlags:maxlags]です。

[c,lags] = xcov(x,maxlags) は、遅れ範囲[-maxlags:maxlags]での自己共分散列を出力します。

[c,lags] = xcov(x,maxlags) は、xがm行p列の配列とすると、[c,lags] = xcov(x,maxlags) は、xの列のすべての組み合わせに対する相互共分散列を含むP²列の2*maxlags+1行をもつ配列cを出力します。

[c,lags] = xcov(x,y,maxlags,'option') は、スケーリングオプションを設定します。ここで、option は、入力引数として最後のものです。

すべての場合、 xcov は、共分散ベクトルのゼロラグが、列の中央、または、mの位置で、maxlag+1行または、要素に位置するように出力します。

例題

プロットするときには、出力遅れを示す2組目の出力引数が有効です。たとえば、つぎのステートメントを使って、一様白色雑音c_ww(m) の推定自己共分散を-10 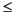m 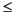10に対して表示することができます。

ww = randn(1000,1);  % 平均 = 1/2の一様白色ノイズを生成
[cov_ww,lags] = xcov(ww,10,'coeff');
stem(lags,cov_ww)

アルゴリズム

xcovは、その入力の平均を計算し、その平均を除去してからxcorrを使います。共分散および相関関数の推定の詳細については、参考文献[1]および[2]を参照してください。

診断

xcovは、入力引数の数以外はエラーチェックを行いません。その代わりに、xcovが呼び出すxcorrのエラーチェックに依存します。

参考

conv
コンボリューションおよび多項式乗算

corrcoef
相関係数行列

cov
共分散行列

xcorr
相互相関関数の推定

xcorr2
2次元相互相関

`conv`	コンボリューションおよび多項式乗算
`corrcoef`	相関係数行列
`cov`	共分散行列
`xcorr`	相互相関関数の推定
`xcorr2`	2次元相互相関

参考文献

[1] Bendat, J.S., and A.G. Piersol, Random Data: Analysis and Measurement Procedures, John Wiley & Sons, New York, 1971, p. 332.

[2] Oppenheim, A.V., and R.W. Schafer, Digital Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1975, pp. 63-67, 746-747, and 839-842.

xcorr2 yulewalk