ss2sos (Signal Processing Toolbox)

状態空間(State space)型から2次型への変換

表示

[sos,g] = ss2sos(A,B,C,D)
[sos,g] = ss2sos(A,B,C,D,iu)
[sos,g] = ss2sos(A,B,C,D,'order')
[sos,g] = ss2sos(A,B,C,D,iu,'order')
[sos,g] = ss2sos(A,B,C,D,iu,'order','scale')
sos = ss2sos(...)

詳細

ss2sosは、与えられたシステムの状態空間(State space)表現を等価な2次型表現に変換します。

[sos,g] = ss2sos(A,B,C,D) は、入力引数A、B、CおよびDによって表現される状態空間(State space)システムと等価なゲインgをもつ2次型形式の行列sosを求めます。入力システムは、単入力かつ実数でなければなりません。sosは、つぎのようなL行6列の行列となります。

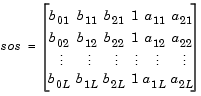
この行は、H(z)の2次型の分子係数b_ikと分母係数a_ikを含みます。

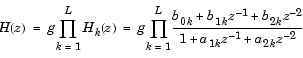
[sos,g] = ss2sos(A,B,C,D,iu) は、状態空間(State space)システムA、B、C、Dのどの出力を変換に使用するかを決定するスカラiuを設定します。iuのデフォルト値は1です。

[sos,g] = ss2sos(A,B,C,D,'order') および

[sos,g] = ss2sos(A,B,C,D,iu,'order') は、sosの行の順序を設定します。ここで、orderには、つぎの文字列が設定できます。

down：sosの最初の行が単位円に最も近い極を含むように並ベます。

up：sosの最初の行が単位円から最も離れた極を含むように並ベます(デフォルト)。

零点は、それに最も近い極と組み合わせることが常です。

[sos,g] = ss2sos(A,B,C,D,iu,'order','scale') は、すべての2次型のゲインと分子の係数を希望するスケーリングを行います。ここで、scaleは、つぎのいずれかを設定することができます。

none：スケーリングを適用しない。

inf：無限大ノルムを適用

two：2ノルムスケーリングを適用

up順序で配置して無限大ノルムスケーリングを使うことにより、実現の中で、オーバフローの可能性を最小にします。また、down順序で配置したものに2ノルムスケーリングを使うことにより、ピークの丸めノイズを最小化します。

sos = ss2sos(...) は、最初の部分H₁(z)に全体のシステムゲインgを埋め込みます。すなわち、つぎのようにします。

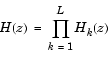
例題

Butterworthローパスフィルタの2次型形式を求めます。

[A,B,C,D] = butter(5,0.2);
sos = ss2sos(A,B,C,D)

sos =
    0.0013    0.0013         0    1.0000   -0.5095         0
    1.0000    2.0008    1.0008    1.0000   -1.0966    0.3554
    1.0000    1.9979    0.9979    1.0000   -1.3693    0.6926

アルゴリズム

ss2sosは、つぎの4つのステップのアルゴリズムを使って入力状態空間(State space)システムの2次型表現を求めます。

A, B, C ,Dによって与えられるシステムの極と零点を求めます。
関数zp2sosを使用します。これは、関数cplxpairを使って、まず零点と極を共役複素数の組に並べ替え、つぎの規則に基づいて極と零点を対応させて、2次型を作成します。
1. 単位円に最も近い極をそれらの極に最も近い零点と組み合わせます。
2. つぎに単位円に近い極をそれらの極に最も近い零点と組み合わせます。
3. 以下同様に続け、極と零点をすべて組み合わせます。

ss2sos は、実数の極と零点についても、絶対値が最も近いものをまとめます。実数の零点に付いても同じルールが適用されます。

極の組み合わせが単位円に近づく具合により、並べ替えます。ss2sosは通常、単位円に最も近い極をもつ断面をカスケードの最後にします。'down'フラグを設定することにより、順序を逆にすることができます。
ss2sosは、引数'scale' で設定されたノルムで、セクションをスケーリングします。任意のH()に対して、スケーリングは、つぎのように定義されます。

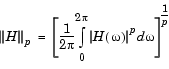
ここで、pは、無限大(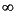)または2のどちらかです。スケーリングの詳細については、参考文献を参照してください。

このスケーリングは、フィルタ処理の中で、いくつかの標準的な固定小数点実現でのオーバフローを最小限に抑えようとするものです。

診断

システムに複数の入力があると、ss2sosは、つぎのエラーメッセージを表示します。

状態空間(State space) system must have only one input.

参考

cplxpair
複素数を共役複素数の組み合わせで並べ替える

sos2ss
ディジタルフィルタの2次型から状態空間(State space)型への変換

ss2tf
状態空間(State space)フィルタパラメータから伝達関数型への変換

ss2zp
状態空間(State space)フィルタパラメータから零点-極-ゲイン型への変換

tf2sos
伝達関数を2次型に変換

zp2sos
ディジタルフィルタの零点-極-ゲイン型から2次型への変換

`cplxpair`	複素数を共役複素数の組み合わせで並べ替える
`sos2ss`	ディジタルフィルタの2次型から状態空間(State space)型への変換
`ss2tf`	状態空間(State space)フィルタパラメータから伝達関数型への変換
`ss2zp`	状態空間(State space)フィルタパラメータから零点-極-ゲイン型への変換
`tf2sos`	伝達関数を2次型に変換
`zp2sos`	ディジタルフィルタの零点-極-ゲイン型から2次型への変換

参考文献

[1] Jackson, L.B., Digital Filters and Signal Processing, 3rd ed., Kluwer Academic Publishers, Boston, 1996. Chapter 11.

[2] Mitra, S.K., Digital Signal Processing: A Computer-Based Approach, McGraw-Hill, New York, 1998. Chapter 9.

[3] Vaidyanathan, P.P.,"Robust Digital フィルタ構造(Filter Structures)," Handbook for Digital Signal Processing, S.K. Mitra and J.F. Kaiser, ed., John Wiley & Sons, New York, 1993, Chapter 7.

square ss2tf