

| Signal Processing Toolbox |   |
表示
y=fft(x) y=fft(x,n)
詳細
fft は、ベクトル、または、行列の離散フーリエ変換を計算します。この関数は、次式で与えられる変換を行います。
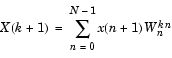
ここで、WN = e-j(2 /N) と N
/N) と N = length(x) です。MATLAB は、0から N-1 の代わりに、1 から N を使うので、この数列は、通常の n と k の代わりに、n +1 と k +1 をインデックスとして使うことに注意してください。
y は、高速フーリエ変換(FFT)アルゴリズムを使って計算された、ベクトル = fft(x)
x の離散フーリエ変換を行います。x が行列の場合、y は、行列の列単位の FFT になります。
y は、 = fft(x,n)
n-点の FFT を行います。x の長さが、n より短い場合、fft は、x にゼロを付加して、長さ n にします。x の長さが、n より長い場合、fft は、数列 x を打ち切ります。x が配列の場合、fft は、同様な方法で、列の長さを調整します。
関数 fft は、MATLAB の基本モジュールの関数です。
例題
フーリエ変換の一般的な使用目的は、時間領域で、雑音の混じった信号の周波数成分を検出することです。1000 Hz でのデータサンプルを考えましょう。50 Hz と 120 Hz の正弦波に平均がゼロのランダム雑音の乗った信号を考えましょう。
randn('state',0)
t = 0:0.001:0.6;
x = sin(2*pi*50*t) + sin(2*pi*120*t);
y = x + 2*randn(1,length(t));
plot(y(1:50))
オリジナルの信号を調べて、周波数成分を識別することは、困難なことです。512点の高速フーリエ変換(FFT) を使って、雑音の混じった信号 y の離散フーリエ変換を行い、周波数領域に変換します。
Y = fft(y,512);
種々の周波数でのエネルギーの尺度になるパワースペクトル密度は、つぎのようにして、求めます。
Pyy = Y.*conj(Y) / 512;
意味をもつ周波数の範囲として、前半 258 点のグラフを表示します。
f = 1000*(0:255)/512;
plot(f,Pyy(1:256))
スペクトル密度の詳細な推定については、関数 pwelch を参照してください。
しばしば、時間領域での単位正弦波が、周波数領域での単位振幅に対応するように、fft の出力を正規化することが有効になります。つぎの手法を使って、正規化された離散時間フーリエ変換を作成します。
Pn = abs(fft(x))*2/length(x)
アルゴリズム
fft は、MATLAB の組み込み関数です。アルゴリズムの詳細については、MATLAB documentation の中の fft リファレンスページを参照してください。
参考
|
離散コサイン変換(DCT) |
|
離散フーリエ変換行列の計算 |
|
2次元高速フーリエ変換 |
|
fft と fft2 の出力の並べ替え |
|
データへのフィルタ操作Filter data. |
|
ディジタルフィルタの周波数応答の計算 |
|
1次元逆高速フーリエ変換 |
|
Welch 法を使った信号のパワースペクトル密度(PSD)の計算 |
 | fdatool | fft2 |  |