Signal Processing Toolbox    
arburg

Burg法を使って、ARモデルパラメータの推定

表示

詳細

a = arburg(x,p) は、Burg法を使って、ARパラメータがLevinson-Durbin再帰法を満足する制約のもとで、前進と後退方向の予測誤差を最小二乗的に満足することにより、p-次の自己回帰(AR)モデルを入力信号xに適合させます。xは、ARモデルに白色ノイズを入力した出力と仮定しています。ベクトルaは、ARシステムパラメータ A(z)の正規化された推定値で、z の降順になっています。

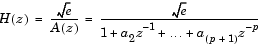
この方法は、全極モデルを使って、入力データを特徴付けるので、モデル次数pの正しい選択が重要になります。

[a,e] = arburg(x,p) は、ARモデルへの白色ノイズ入力の分散eを出力します。

[a,e,k] = arburg(x,p) は、反射係数のベクトルkを出力します。

参考
arcov     共分散法を使って、ARモデルパラメータの推定
armcov    修正共分散法を使って、ARモデルパラメータの推定
aryule    Yule-Walker法を使って、ARモデルパラメータの推定
lpc        線形予測係数の計算
pburg     Burg法を使ったパワースペクトルの推定
prony     時間領域IIRフィルタ設計に対するProny法


 angle arcov