Signal Processing Toolbox

lpc

線形予測係数

表示

a = lpc(x,p)

詳細

lpcは、最小二乗的に予測誤差を最小にすることで、前置型線形予測子の係数を決定します。

a = lpc(x,p) は、過去のサンプルをベースに実数値時系列x のカレント値を予測するp次の線形予測子(FIRフィルタ)の係数を決定します。

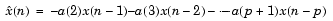
ここで、pは、予測多項式の次数です。 a = [1 a(2) ... a(p+1)]

pを設定していない場合、lpcはデフォルトの p = length(x)-1を使います。xが列単位に別々の信号を含んだ行列の場合、lpcは行列aの各行に各列に対するモデルの推定値を出力します。

例題

3次の前置予測子を使って、データ列を計算し、オリジナル信号と比べましょう。

まず、白色ノイズにより、励起された自己回帰プロセス出力を信号データとして作成します。最初の遷移部を避けるため、ARプロセス出力の項範の4096サンプルを使います。

randn('state',0);
noise = randn(50000,1);  % 正規化された白色ガウスノイズ
x = filter(1,[1 1/2 1/3 1/4],noise);
x = x(45904:50000);

予測子係数、指定した信号、予測誤差、予測誤差の自己相関列を比較します。

a = lpc(x,3);
est_x = filter([0 -a(2:end)],1,x);    % 推定した信号
e = x - est_x;                        % 予測誤差
[acs,lags] = xcorr(e,'coeff');        % 予測誤差のACS 

予測誤差e(n)は、つぎに示す予測誤差フィルタA(z)の出力と考えられます。ここで、H(z)は最適線形予測子、x(n)は入力信号、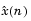は予測信号です。

予測した信号とオリジナル信号を比較しましょう。

plot(1:97,x(4001:4097),1:97,est_x(4001:4097),'--');
title('Original Signal vs. LPC Estimate');
xlabel('Sample Number'); ylabel('Amplitude'); grid;
legend('Original Signal','LPC Estimate')

予測誤差の自己相関列を調べましょう。

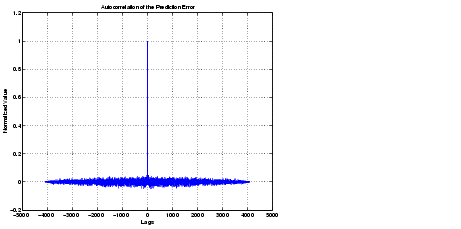
plot(lags,acs); 
title('Autocorrelation of the Prediction Error');
xlabel('Lags'); ylabel('Normalized Value'); grid;

予測誤差は、3次のAR入力プロセスに対して期待したように、近似的に白色ガウスノイズになっています。

アルゴリズム

lpcは、自己回帰(AR)モデリングの自己相関法を使って、フィルタ係数を求めます。この手法は、スペクトル推定の最大エントロピ法(MEM)とも呼ばれます。生成されるフィルタは安定です。しかし、生成されるフィルタは、たとえデータ列が正しい次数のAR過程であっても、過程を正確にモデリングしない可能性があります。これは、自己相関法がデータへのウィンドウ適用を行っているため、すなわち、xの長さを越える信号サンプルは0であると仮定しているためです。

lpcは、つぎの方程式の最小二乗解を計算します。

ここで、

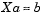
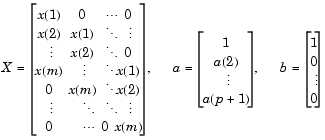
mは、xの長さです。正規方程式として、最小二乗問題を解くことは、

Yule-Walker方程式を導くことになります。

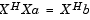
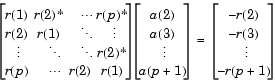
ここで、 r = [r(1) r(2) ... r(p+1)] は、xcorrを使って計算するxに対する自己相関推定です。Yule-Walker方程式は、Levinson-Durbinアルゴリズム(levinsonを参照)を使って、O(p²)フロップスで解かれます。

参考

aryule	Yule-Walker法を使ったARモデルパラメータの推定
levinson	Levinson-Durbin再帰法での計算
prony	Prony法を使った時間領域IIRフィルタ設計
pyulear	Yule-Walker AR法を使ったパワースペクトル密度の計算
stmcb	Steiglitz-McBride法を使った線形モデル

参考文献

[1] Jackson, L.B., Digital Filters and Signal Processing, Second Edition, Kluwer Academic Publishers, 1989. pp. 255-257.

lp2lp

lsf2poly