Control System Toolbox関数リファレンス

gram

可制御性グラミアンおよび可観測性グラミアン

表示

Wc = gram(sys,'c')
Wo = gram(sys,'o')

詳細

gram は、可制御性グラミアンおよび可観測性グラミアンを計算します。グラミアンは、状態空間モデルの可制御性や可観測性の特性を調べたり、モデルの低次元化[1]を行なうのに使用することができます。可制御性グラミアンや可観測性グラミアンは、ctrbやobsvで作成した可制御性行列や可観測性行列より優れた数値特性をもっています。

つぎの連続系状態空間モデルが与えられた場合、

可制御性グラミアンは、

によって定義され、可観測性グラミアンは、

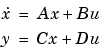
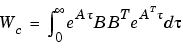
によって定義されます。離散系の可制御性グラミアンおよび可観測グラミアンは、つぎのとおりです。

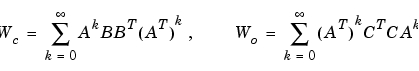
可制御性グラミアンは、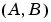が可制御の場合に限り、正定です。同様に、可観測性グラミアンは 、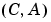が可観測の場合に限り、正定です。

つぎのコマンドを使って、連続系または離散系のグラミアンを計算します。

Wc = gram(sys,'c')    % 可制御性グラミアン
Wo = gram(sys,'o')    % 可観測性グラミアン

LTIモデルsysは、状態空間型でなければなりません。

アルゴリズム

可制御性グラミアン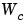は、つぎの連続系Lyapunov方程式を解くことによって得られます。

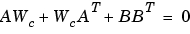
あるいは、つぎの離散系Lyapunov方程式を解くことによって得られます。

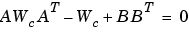
同様に、可観測性グラミアン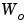は、連続系において、つぎのLyapunov方程式を解くことによって得られます。

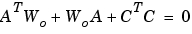
また、離散系の場合は、つぎのLyapunov方程式を解くことによって得られます。

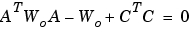
制限

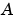行列は、安定でなければなりません(すべての固有値は、連続系において実部は負で、離散系においては大きさが1未満です)。

参考
balreal     状態実現のグラミアンをベースにした平衡化

ctrb        可制御性行列

lyap, dlyap Lyapunov方程式の解法ソルバ

obsv        可観測性行列

参考文献

[1] Kailath, T., Linear Systems, Prentice-Hall, 1980.

get

hasdelay