

| Control System Toolbox関数リファレンス |   |
表示
X = lyap(A,Q) X = lyap(A,B,C)
詳細
lyap
は、特殊、および一般形式のLyapunov行列方程式を解きます。Lyapunov方程式は、安定性理論およびシステムのRMS挙動の研究など多くの制御分野で使われています。
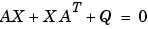
を解きます。ここで、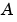 と
と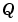 は、同じ大きさの正方行列です。
は、同じ大きさの正方行列です。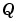 が対称行列の場合、解
が対称行列の場合、解Xも対称行列になります。
X = lyap(A,B,C)
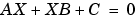
行列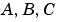 は、お互いの次元に整合性が必要ですが、正方行列である必要はありません。
は、お互いの次元に整合性が必要ですが、正方行列である必要はありません。
アルゴリズム
lyapは、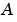 、
、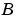 行列を複素Schur型に変換し、結果の三角システムの解を計算し、この解を逆変換により戻します[1]。
行列を複素Schur型に変換し、結果の三角システムの解を計算し、この解を逆変換により戻します[1]。
制限
連続系Lyapunov方程式は、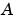 の固有値
の固有値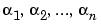 および
および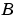 の固有値
の固有値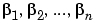 が、すべての
が、すべての(i,j)の組に対して、αi+βjが0でない場合、(一意的な)解をもちます。この条件に反すると、lyapは、つぎのエラーメッセージを表示します。
Solution does not exist or is not unique.
参考
covar 白色ノイズに対するシステム応答の共分散
dlyap 離散系Lyapunov方程式の解法ソルバ
参考文献
[1] Bartels, R.H. and G.W. Stewart, "Solution of the Matrix Equation AX + XB = C," Comm. of the ACM, Vol. 15, No. 9, 1972.
[2] Bryson, A.E. and Y.C. Ho, Applied Optimal Control, Hemisphere Publishing, 1975. pp. 328-338.
 | ltiview | margin |  |