| MATLAB Function Reference | |
表示
[A,B,C,...] = gallery('tmfun',P1,P2,...)
gallery(3) 条件数の悪い 3行3列行列gallery(5) 興味深い固有値問題
詳細
[A,B,C,...] は、文字列 = gallery('tmfun',P1,P2,...)
tmfun で指定されるテスト行列を出力します。 tmfun は、下記の表から選択される行列のファミリ名です。P1, P2,... は、個々の行列ファミリが必要とする入力パラメータです。シンタックスのコールで使われるオプションパラメータ P1,P2,... の数は、行列ごとに変化します。正確な呼び出しシンタックスは、下記の個々の行列についての説明で、詳細を示します。
gallery は、アルゴリズムのテストやその他の目的に対して、便利な50以上の異なるテスト行列関数を保持しています。
cauchy--Cauchy 行列
C = gallery('cauchy',x,y)
は、C(i,j)
= 1/(x(i)+y(j)) であるn行n列の行列を出力します。引数 x と y は、長さが n のベクトルです。x と y に対してスカラを与えると、それらは、1:x、および、1:y のベクトルとして解釈されます。
C = gallery('cauchy',x)
は、y = x として、上記と同様な出力を行います。すなわち、このコマンドは、C(i,j) = 1/(x(i)+x(j)) を出力します。
Cauchy行列の逆行列および行列式に対しては、明示的な公式が知られています。x と y がどちらも異なる要素をもつ場合、行列式 det(C) は非ゼロです。0 < x(1) <... < x(n)、かつ、0 < y(1) < ... < y(n) ならば、C は完全に正です。
chebspec--Chebyshev スペクトル差分行列
C = gallery('chebspec',n, は、switch)
n次の Chebyshevスペクトル微分行列を出力します。引数 switch は、出力行列の特性を決定する変数です。デフォルトでは、switch = 0 です。
For switch = 0 ("境界条件なし")に対して、C はべき零(Cn = 0)で、空ベクトル ones(n,1) をもちます。行列 C は、零の固有値をもつサイズ n の Jordanブロックに相似です。
switch = 1, C に対して、C は正則で、条件数がよく、その固有値は負の実部をもちます。
Chebyshevスペクトル微分行列の固有ベクトル行列 V は、条件数がよくありません。
chebvand--Chebyshev 多項式用の Vandermonde 行列に似た行列
C = gallery('chebvand',p)
は、Chebyshev多項式を計算する点を定義する点 p からなるベクトルに基づいて(主要な)Chebyshev Vandermonde 行列を生成します。
C = gallery('chebvand',m,p)
は、m がスカラのとき、m行の上記の長方形バージョンを生成します。
p がベクトルの場合、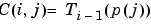
です。ここで、
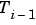は、i-1次の Chebyshev多項式です。p がスカラの場合、区間 [0,1]上で等間隔に分布する p点が C を計算するために使われます。
chow--正則でない Toeplitz 下 Hessenberg 行列
A = gallery('chow',n,alpha,delta)
は、A = H(alpha) + delta*eye(n) であるような A を出力します。ここで、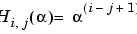
です。引数 n は Chow行列の次数で、一方、alpha と delta は、それぞれデフォルト値が 1 と 0 のスカラです。
H(alpha) は、ゼロに等価な p = floor(n/2)個の固有値をもちます。残りの固有値は、4*alpha*cos(k*pi/(n+2))^2, k=1:n-p に等価です。
circul-- 循環行列
C = gallery('circul',v)
は、最初の行がベクトル v である循環行列を出力します。
循環行列は、１ステップ前のエントリを循環的に置換することによって、１つ前の行から各行が得られるという性質をもっています。これは、対角要素が"囲まれた"、特別な Toeplitz行列です。
vがスカラの場合、C = gallery('circul',1:v)です。
C (n行n列) の固有システムは明示的に知られています。tが、n 番目の単位根であれば、v と w = [1 t t2 ... tn] との内積は、C の固有値で、 w(n:-1:1) は、固有ベクトルです。
clement-- ゼロを対角要素とする三角行列
A = gallery('clement',n,sym)
は、主対角にゼロをもち、既知の固有値をもつ n 行 n 列の三角行列を出力します。次数 n が、奇数の場合、正則でなくなります。逆行列の要素の約64パーセントはゼロになります。固有値は、(n が奇数に対して)1、または、0 の最終的な固有値と同様に、プラス、マイナスの数字 n-1, n-3, n-5, ... を含みます。
引数 sym は、Clement行列が対称かどうかを決定します。sym = 0 (デフォルト)の場合、行列は非対称ですが、sym = 1 の場合、対称です。
compar--Comparison 行列
A = gallery('compar',A,1)
は、対角要素はその絶対値で置き換えられ、非対角要素は、各行の中の要素の絶対値の最大値にマイナスを付けた値で置き換えられた A行列を出力します。しかし、A が三角行列の場合、compar(A,1) も三角行列になります。
gallery('compar',A) は、diag(B) - tril(B,-1) - triu(B,1) で、ここで、B = abs(A) です。compar(A) は、文献ではしばしば M(A) と記述されます。
gallery('compar',A,0) は、compar(A) と同じです。
condex--Counter-examples to matrix condition number estimators
A = gallery('condex',n,k,theta)
は、条件数の推定に対する"counter-example"行列を出力します。これは、次数 nとスカラパラメータ theta (デフォルト100) をもちます。
この行列のサイズと適用する推定法は、つぎのように、k によって指定されます。
k = 1 |
4 行 4 列 |
LINPACK (rcond) |
k = 2 |
3 行 3 列 |
LINPACK (rcond) |
k = 3 |
任意 |
LINPACK (rcond) (theta に独立) |
k = 4 |
n  4 |
SONEST (Higham 1988) (デフォルト) |
n が妥当な行列サイズでなければ、次数 n に対して単位行列が加えられます。
cycol--Matrix whose columns repeat cyclically
A = gallery('cycol',[m n],k)
は、循環する反復列からなるm行n列の行列を出力します。ここで、1サイクルはrandn(m,k) です。つまり、行列 A のランクは、k を超えることはありません。kは、スカラでなければなりません。
引数 k のデフォルトは、round(n/4)ですが、n を割り切る必要はありません。
A = gallery('cycol',n,k),
ここで、n はスカラで、gallery('cycol',[n n],k)と同じです。
dorr--Diagonally dominant, ill-conditioned, tridiagonal matrix
[c,d,e] = gallery('dorr',n,theta)
は、小さな非負値 theta に対して、条件数の悪い次数 n の三重対角行列の各対角要素を定義するベクトルを出力します。theta
のデフォルト値は 0.01 です。Dorr行列自身は、gallery('tridiag',c,d,e)
と同じです。
A = gallery('dorr',n,theta)
は、ベクトルではなく行列を出力します。
dramadah--Matrix of zeros and ones whose inverse has large integer entries
A = gallery('dramadah',n,k)
は、mu(A) = norm(inv(A),'fro') が相対的に大きくなるような(最大である必要はありません)、n行n列の行列を出力します。反Hadamard行列 A は、mu(A) が最大となる、0 と 1 の要素をもつ行列です。
n と kは、共にスカラでなければなりません。引数 kは、出力行列の特性を決定します。
fiedler--対称行列
A = gallery('fiedler',c),
は、cが、長さ n のベクトルのとき、要素 abs(n(i)-n(j))をもつ n行n列の対称行列を出力します。スカラ c に対して、A = gallery('fiedler',1:c)です。
行列 Aは、主要な一つの正の固有値をもち、それ以外の固有値はすべて負です。
[Todd, J., Basic Numerical Mathematics, Vol. 2: Numerical Algebra, Birkhauser, Basel, and Academic Press, New York, 1977, p. 159] に記載されている inv(A)と det(A) に対する明示的な式は、Fiedler によって考えられたものです。これらは、非ゼロの(1,n)要素と (n,1)要素を除いて、inv(A)が三重対角行列であることを示しています。
forsythe--Perturbed Jordan block
A = gallery('forsythe',n,alpha,lambda)
は、A(n,1) = alphaであることを除いて、固有値 lambda をもつ Jordanブロックに等価な n行n列の行列を出力します。スカラalpha と lambdaのデフォルト値は、それぞれ、sqrt(eps)と0 です。
det(A-t*I) = (lambda-t)^N - alpha*(-1)^n.
frank--Matrix with ill-conditioned eigenvalues
F = gallery('frank',n,k)
は、次数n の Frank行列を出力します。これは、行列式が1 の上Hessenberg行列です。k = 1ならば、各要素は反対角成分(1,n)--(n,1)について反映されます。Fの固有値は、エルミート多項式の零点として得られることがあります。これらの固有値は正で、双対の組合わせが存在します。nが奇数ならば、一つの固有値は 1です。F は、条件数の悪い floor(n/2)個の固有値をもちます。それらは、1 より小さな値です。
gearmat--Gear matrix
A = gallery('gearmat',n,i,j)
は、主対角よりも一つ上側と下側の対角要素が 1、(1,abs(i))要素がsign(i)、(n,n+1-abs(j))要素が sign(j)、それ以外が 0 のn行n列の行列を出力します。引数
i と j のデフォルト値は、それぞれ n と -n
です。
A は特異行列で、2重および 3重の固有値をもつことも、不完全(defective)になることもあります。
固有値は、すべて 2*cos(a)の型で、固有ベクトルは [sin(w+a), sin(w+2a), ..., sin(w+Na)] の型です。ここで、aと w は、 Gear, C. W., "A Simple Set of Test Matrices for Eigenvalue Programs", Math. Comp.,Vol. 23 (1969), pp. 119-125 で与えられています。
grcar--Toeplitz matrix with sensitive eigenvalues
A = gallery('grcar',n,k)
は、主対角よりも一つ下側の対角要素が-1 で、主対角と上側 k番目までの対角要素が1 である、n行n列の Toeplitz行列を出力します。デフォルトでは、k = 3 です。これは、敏感な固有値をもちます。
hanowa--Matrix whose eigenvalues lie on a vertical line in the complex plane
A = gallery('hanowa',n,d)
は、つぎのような2行2列のブロック行列からなるn行n列の行列を出力します。
[d*eye(m) -diag(1:m) diag(1:m) d*eye(m)]
引数 n は、偶数 n=2*mです。行列 A は、d ± k*i型(1 <= k <= m)の複素固有値をもちます。dのデフォルト値は -1 です。
house--Householder matrix
[v, beta] = gallery('house',x)
は、スカラ、または、n要素の列ベクトル x を使って、eye(n,n)- beta*v*v' が、 Householder行列であるような、vと beta を出力します。Householder行列 Hは、つぎの関係を満足します。
H*x = -sign(x(1))*norm(x)*e1
ここで、e1 は、eye(n,n)の最初の列です。x が複素数の場合、sign(x) = exp(i*arg(x)) (これは xが非ゼロのとき、x./abs(x) と等価)であることに注意してください。
x = 0 の場合、v = 0 と beta = 1 になります。
invhess--Inverse of an upper Hessenberg matrix
A = gallery('invhess',x,y),
は、xが長さ n のベクトルで yが長さ n-1 のベクトルのとき、下三角部分が
ones(n,1)*x' の下三角部分に等しく、主対角よりも上側の三角部分が
[1 y]*ones(1,n)の上三角部分に等しい行列を出力します。
すべての i に対して、 x(1) ~= 0 かつ x(i+1) ~= y(i) の場合、この行列は正則で、逆行列は上Hessenberg行列です。引数y のデフォルト値は、-x(1:n-1)です。
x がスカラの場合、invhess(x)は、invhess(1:x) と同じです。
invol--Involutory matrix
A = gallery('invol',n)
は、n行n列のinvolutory (A*A = eye(n))かつ条件数の悪い行列を出力します。これは、hilb(n)を対角的にスケーリングしたものです。
B = (eye(n)-A)/2、および、B = (eye(n)+A)/2は、(B*B = B) を満たします。
ipjfact--Hankel matrix with factorial elements
[A,d] = gallery('ipjfact',n,k)
は、n行n列の Hankel行列 A と、明示的に知られているA の行列式 d を出力します。k = 0 (デフォルト)の場合、Aの要素は、A(i,j) = (i+j)! です。k = 1 の場合、A の要素は、A(i,j) = 1/(i+j)です。
jordbloc--Jordan block
A = gallery('jordbloc',n,lambda)
は、固有値 lambda をもつ n 行 n 列の Jordan ブロックを出力します。lambda のデフォルト値は、1 です。
kahan--Upper trapezoidal matrix
A = gallery('kahan',n,theta,pert)
は、条件数およびランクの推定に関して興味深い性質をもつ上台形行列を出力します。
n が 2要素ベクトルの場合、Aは n(1)行n(2)列で、そうでなければ、A は、n行n列の行列です。thetaの有効な範囲は、0 < theta < piで、デフォルト値は 1.2 です。
列のピボットによる QR分解が、丸め誤差の存在する列を交換しないようにするために、対角要素に、pert*eps*diag([n:-1:1])として摂動を与えます。デフォルトの pert は 25 で、IEEE演算では、少なくとも n = 90 までの gallery('kahan',n) に対して、列の交換が行われないことが保証されています。
kms--Kac-Murdock-Szego Toeplitz matrix
A = gallery('kms',n,rho)
は、実数rho に対して、A(i,j) = rho^(abs(i-j))であるようなn行n列のKac-Murdock-Szego Toeplitz行列を出力します。
複素数 rhoに対しては、主対角より下側の要素が共役複素数であることを除いて、同じ式を保持します。rhoのデフォルト値は 0.5 です。
L = inv(triw(n,-rho,1)') と D(i,i) = (1-abs(rho)^2)*eye(n)(ただし、D(1,1) = 1)によって LDL分解が可能です。0 < abs(rho) < 1 の場合に限り、正定値です。 inv(A) は、三重対角行列です。krylov--Krylov matrix
B = gallery('krylov',A,x,j)
は、Krylov行列
[x, Ax, A^2x, ..., A^(j-1)x]
を出力します。A は n行n列の行列で、x は、長さ n のベクトルです。デフォルトは、x = ones(n,1) と j = n です。
B = gallery('krylov',n)
は、gallery('krylov',(randn(n))と同じです。
lauchli--Rectangular matrix
A = gallery('lauchli',n,mu)
は、(n+1)行n列の行列
[ones(1,n); mu*eye(n)]
を出力します。Lauchli行列は、A'*Aの形成に危険を示す、最小二乗およびその他の問題において、よく知られた例題です。引数mu のデフォルト値は sqrt(eps)です。
lehmer--Symmetric positive definite matrix
A = gallery('lehmer',n)
は、j>= i に対して A(i,j) = i/jであるようなn行n列の対称正定行列を出力します。
A は、完全に非負です。inv(A) は、三重対角行列で、明示的に知られています。n <= cond(A) <= 4*n*n です。lesp--Tridiagonal matrix with real, sensitive eigenvalues
A = gallery('lesp',n)
は、固有値が実数で、かつ、ほぼ
[-2*N-3.5, -4.5]区間で滑らかに分布するn行n列の行列を出力します。
固有値が大きな負の値になるに連れて、その感度は指数的に大きくなります。行列は、D = diag(1!,2!,...,n!) を使った相似変換により、対角要素が同じで、非対角要素が 1 の対称三重対角行列と相似です。
lotkin--Lotkin matrix
A = gallery('lotkin',n)
は、最初の行が、すべて
1 である Hilbert行列を出力します。Lotkin行列 Aは、非対称で条件数が悪く、小さな負の固有値を多数もちます。その逆行列は整数要素をもち、明示的に知られています。
minij--Symmetric positive definite matrix
A = gallery('minij',n)
は、A(i,j) = min(i,j) の n行n列の対称正定行列を出力します。
inv(A) は三重対角行列で、(n,n)要素が 1 であることを除いて、2階差分行列を -1 倍したものに等価です。2*A-ones(size(A)) は、三重対角の逆行列をもち、固有値は r=1:n に対して、0.5*sec((2*r-1)*pi/(4*n))^2 です。(n+1)*ones(size(A))-A は、max(i,j) を要素としてもち、その逆行列は三重対角行列です。moler--Symmetric positive definite matrix
A = gallery('moler',n,alpha)
は、n行n列の対称正定行列 U'*U を出力します。ここで、U = triw(n,alpha) です。
デフォルト alpha = -1に対して、A(i,j) = min(i,j)-2 かつ A(i,i) = i です。A の固有値の一つは小さな値をもちます。
neumann--Singular matrix from the discrete Neumann problem (sparse)
C = gallery('neumann',n)
は、規則的なメッシュ上の通常の5点演算子を使って、 Neumann問題を離散化した結果として、特異な行対角主要行列を出力します。引数n は、完全な 2乗整数 n = m2、または 2要素ベクトルです。Cは、スパース行列で、空ベクトル ones(n,1)について 1次元のヌル空間をもちます。
orthog--Orthogonal and nearly orthogonal matrices
Q = gallery('orthog',n,k)
は、次数n の k番目のタイプの行列を出力します。ここで、k> 0 は、正確な直交行列を選択し、k < 0 は、対角スケーリングされた直交行列を選択します。以下のタイプを指定できます。
parter--Toeplitz matrix with singular values near pi
C = gallery('parter',n)
は、C(i,j) = 1/(i-j+0.5) であるような行列 Cを出力します。
Cは、Cauchy行列かつ Toeplitz行列です。Cの特異値のほとんどは、非常にπに近い値です。
pei--Pei matrix
A = gallery('pei',n,alpha),
は、alphaがスカラのとき、対称行列 alpha*eye(n) + ones(n) を出力します。alphaのデフォルト値は 1 です。0 または、 -nに等しい alpha に対して、特異行列になります。
poisson--Block tridiagonal matrix from Poisson's equation (sparse)
A = gallery('poisson',n)
は、n行n列のメッシュ上の5点演算子を使って Poisson方程式を離散化した結果として、次数n^2 のブロック三重対角(スパース)行列を出力します。
prolate--Symmetric, ill-conditioned Toeplitz matrix
A = gallery('prolate',n,w)
は、パラメータw を使って、 n行n列のprolate行列を出力します。結果は、対称な Toeplitz行列です。
Aの固有値は、すべて異なり、(0,1)内に存在します。その中で、0 と 1 の近傍に分類される傾向があります。w のデフォルト値は 0.25 です。randhess--Random, orthogonal upper Hessenberg matrix
H = gallery('randhess',n)
は、n行n列の実数のランダムな直交上Hessenberg行列を出力します。
H = gallery('randhess',x)
x が、長さ n (n > 1)の任意の実数ベクトルならば、H = gallery('randhess',x) は、 x の要素をパラメータとして使ってランダムでない行列 H を作成します。
行列 H は、n-1次の Givens回転行列の積によって作られます。
rando--Random matrix composed of elements -1, 0 or 1
A = gallery('rando',n,k)
は、つぎのいずれかの離散分布よる要素をもつ、ランダムな
n行n列の行列を出力します。
k = 1 |
等しい確率で、A(i,j) = 0 、または 1 となります(デフォルト>)。 |
k = 2 |
等しい確率で A(i,j) = -1 、または、 1 となります。 |
k = 3 |
等しい確率で、A(i,j) = -1, 0 1 となります。 |
引数 n は、2要素ベクトルでも構いません。この場合、n(1)行n(2)列の行列になります。
randsvd--Random matrix with preassigned singular values
A = gallery('randsvd',n,kappa,mode,kl,ku)
は、cond(A) = kappaと分布モードによる特異値をもつn次のランダム帯(多重対角)行列を出力します。nが、2要素ベクトルの場合、A は、 n(1)行n(2)列の行列です。
引数 kl と ku は、それぞれ Aの主対角の上側と下側の対角の数を指定します。省略するとフル行列が生成されます。klのみを与えると、ku は、 klをデフォルトとします。
条件数 kappa のデフォルト値は、sqrt(1/eps)です。kappa < 0 の特別な場合では、Aは、cond(A) = -kappa で modeに従って分布する固有値をもつ、ランダムな対称正定フル行列です。引数kl と kuは、存在しても無視されます。
redheff--Redheffer's matrix of 1s and 0s
A = gallery('redheff',n)
は、j = 1、または、i が j を割り切る場合、A(i,j) = 1 で、それ以外では、 A(i,j) = 0 と定義される 0 と 1 からなる n行n列の行列を出力します。
(n-floor(log2(n)))-1個の固有値は、1に等価です。sqrt(n) です。 -sqrt(n)です。> 0 に対して、det(A) = O(n^(1/2+epsilon)) であるときのみ、Riemann仮説は真です。Barrett と Jarvisは、小さな固有値は単位円 abs(Z) = 1 の内部に存在すると推測し、この推測の証明は、nが大きくなるに連れて、ある固有値は零に近づくことの証明と共に、素数定理の新たな証明を生み出しています。
riemann--Matrix associated with the Riemann hypothesis
A = gallery('riemann',n)
は、すべてのepsilon > 0 に対して、det(A) = O(n! n^(-1/2+epsilon)) のときのみ Riemann仮説が真である n行n列の行列を出力します。
A = B(2:n+1,2:n+1)
ここで、i が j を割り切る場合 B(i,j) = i-1で、それ以外では B(i,j) = -1 です。
e(i) は、 abs(e(i)) <= m-1/m を満足します。ここで、 m = n+1 です。i <= e(i) <= i+1 です。例外は多くても m-sqrt(m)個です。(m/3, m/2]内のすべての整数が固有値です。ris--Symmetric Hankel matrix
A = gallery('ris',n)
は、対称なn行n列の Hanke行列を出力します。つぎの要素をもちます。
A(i,j) = 0.5/(n-i-j+1.5)
A の固有値は、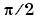
と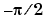 
の周囲に分類されます。この行列は、 F.N. Ris によって考えられました。
rosser--Classic symmetric eigenvalue test matrix
A = rosser
は Rosser行列を出力します。この行列は、多くの行列固有値アルゴリズムに対する課題でした。しかし、Wilkinsonによって完成され、EISPACK や MATLAB で実現されたように、Francis の QRアルゴリズムでは問題がありません。これは、整数要素をもつ8行8列の行列です。以下の固有値をもちます。
smoke--Complex matrix with a 'smoke ring' pseudospectrum
A = gallery('smoke',n)
は、主対角より一つ上側の対角要素と(n,1)要素が 1 で、対角上の各要素が単位円上のべき乗根であるn行n列の行列を出力します。
A = gallery('smoke',n,1)
は、A(n,1)がゼロであることを除いて同じ行列を出力します。
smoke(n,1)の固有値は単位円上の n番目の根です。smoke(n)の固有値は、単位円上の n番目の根を 2^(1/n)倍したものです。
toeppd--Symmetric positive definite Toeplitz matrix
A = gallery('toeppd',n,m,w,theta)
は、 n行n列の対称な準正定(SPD)Toeplitz行列を出力します。行列は、 m の rank 2 (または、特定のtheta に対しては rank 1)の SPD Toeplitz行列の和から構成されます。特に、
T = w(1)*T(theta(1)) + ... + w(m)*T(theta(m))
ここで、T(theta(k)) の (i,j)要素は、cos(2*pi*theta(k)*(i-j))です。
デフォルトでは、m = n, w = rand(m,1), theta = rand(m,1)です。
toeppen--Pentadiagonal Toeplitz matrix (sparse)
P = gallery('toeppen',n,a,b,c,d,e)
は、それぞれの対角成分が、 P(3,1) = a, P(2,1) = b, P(1,1) = c, P(1,2) = d, P(1,3) = e のn行n列のスパースな五重対角Toeplitz行列を出力します。ここで、a,b, c, d, e は、スカラです。
デフォルトは、(a,b,c,d,e) = (1,-10,0,10,1) で、Rutishauser の行列を生成します。この行列は、ほぼ、ラインセグメント2*cos(2*t) + 20*i*sin(t)上に固有値をもちます。
tridiag--Tridiagonal matrix (sparse)
A = gallery('tridiag',c,d,e)
は、主対角よりも一つ下側の対角要素が c、主対角要素が d、一つ上側の対角要素がe である、三重対角行列を出力します。ベクトルc と e は、長さが length(d)-1でなければなりません。
A = gallery('tridiag',n,c,d,e),
は、c, d, e が、すべてスカラの場合、一つ下側の対角要素がc、主対角要素が d、一つ上側の対角要素がe である、次数 n の Toeplitz三重対角行列を生成します。この行列は、つぎの固有値をもちます。
d + 2*sqrt(c*e)*cos(k*pi/(n+1))
A = gallery('tridiag',n)
は、A = gallery('tridiag',n,-1,2,-1) と同じで、対称な正定 M-行列です(2階差分行列の負)。
triw--Upper triangular matrix discussed by Wilkinson and others
A = gallery('triw',n,alpha,k)
は、主対角要素が 1 で、k(>= 0)番目までの上側対角要素が、alphas の上三角行列を出力します。
次数 n は 2要素ベクトルでも構いません。この場合、n(1)行(2)列の上台形行列になります。
Ostrowski ["On the Spectrum of a One-parametric Family of Matrices, J. Reine Angew. Math., 1954] は、以下のことを示しています。
cond(gallery('triw',n,2)) = cot(pi/(4*n))^2,
かつ、大きな abs(alpha) に対して、cond(gallery('triw',n,alpha)) は、およそ abs(alpha)^n*sin(pi/(4*n-2))です。
(n,1)要素に -2^(2-n)を加えると triw(n) は特異行列になります。最初の列のすべての要素に-2^(1-n) を加えても同様です。
vander--Vandermonde matrix
A = gallery('vander',c)
は、最後から2番目の列が c である Vandermonde行列を出力します。Vandermonde行列のj番目の列は A(:,j) = C^(n-j)で与えられます。
wathen--Finite element matrix (sparse, random entries)
A = gallery('wathen',nx,ny)
は、スパースでランダムなn行n列の有限要素行列を出力します。ここで、つぎのようになります。
n = 3*nx*ny + 2*nx + 2*ny + 1.
行列 A は、2つの次元において、8-ノード(serendipity)要素からなる規則的な nx行ny列グリッドに対して、正確に"矛盾のないマス行列" です。A は、このルーチンの中でランダムに選ばれる任意の(正の)"密度" rho(nx,ny) に対して、対称な正定行列です。
A = gallery('wathen',nx,ny,1)
は、つぎを満たすように対角にスケーリングされた行列を出力します。
0.25 <= eig(inv(D)*A) <= 4.5
ここで、任意の正の整数 nx、ny と任意の密度 rho(nx,ny) に対して、D = diag(diag(A)) です。
wilk--Various matrices devised or discussed by Wilkinson
[A,b] = gallery('wilk',n)
は、nの値に応じて、異なる行列または線形システムを出力します。
参考
hadamard, hilb, invhilb, magic, wilkinson
参考文献
MATLAB のテスト行列のギャラリは、英国のManchester にある University of Manchester の数学部門でのNicholas J. Highamの作業に基づいています。これらの行列についての詳細は、N. J. Higham による The Test Matrix Toolbox for MATLAB (Version 3.0) , September, 1995 に記載されています。このレポートを pdf書式で入手するためには、MATLABプロンプトでコマンド doc を入力し、Help Desk のメインのスクリーン上のFull Documentation Set項目から Related Papers の Test Matrix Toolboxを選択してください。このレポートは、The MathWorks の anonymous ftpサイト(/pub/contrib/v5/linalg/testmatrix/testmatrix.ps)、あるいは、World Wide Web ( ftp://ftp.ma.man.ac.uk/pub/narep、または、http://www.ma.man.ac.uk/MCCM/MCCM.html) から入手することもできます。さらに、その背景については、文献 "Accuracy and Stability of Numerical Algorithms, Nicholas J. Higham, SIAM, 1996." を参照してください。
| | fzero | gamma, gammainc, gammaln | |