fzero (MATLAB Function 参考文献)

1 変数関数の零点を求めます。

表示

x = fzero(fun,x0)
x = fzero(fun,x0,options)
x = fzero(fun,x0,options,P1,P2,...)
[x,fval] = fzero(...)
[x,fval,exitflag] = fzero(...)
[x,fval,exitflag,output] = fzero(...)

詳細

x = fzero(fun,x0) は、x0 がスカラの場合、x0 の近傍で、fun の零点を求めます。fzero で戻される値 x は、fun の符号の変化する点の近傍で、探索が失敗した場合は、NaN を出力します。この場合、Inf、NaN、複素数が求まらなくなるまで、探索範囲を広げたときに、探索は終了します。

x0 が長さ2のベクトルの場合、fzero は、x0は、fun(x0(1)) の符号は、fun(x0(2))の符号と変わる区間を表します。このような範囲でない場合は、エラーが生じます。このような区間と共にfzeroをコールすることは、fzeroが、fun の符号が変化する点の近傍での値を出力することを保証することになります。

x = fzero(fun,x0,options) は、構造体 options に指定した最適化パラメータを使って、最小化します。これらのパラメータは、関数optimset を使って定義します。fzero は、つぎの options 構造体フィールドを使います。

Display - 表示レベル。off は、表示を行いません。 iter は、各繰り返し毎に出力を表示します。final は、最終結果のみを表示します。

TolX - x に関する終了トレランス

x = fzero(fun,x0,options,P1,P2,...) は、付加引数を関数 fun に渡します。オプションを設定しない場合は、options = [] を使います。

[x,fval] = fzero(...) は、解 x で、目的関数 fun の値を出力します。

[x,fval,exitflag] = fzero(...) は、fzero の終了条件を示す値 exitflag を出力します。

> 0 は、関数が、零点になる x を見つけたことを示します。

< 0 の場合、指定した区間で、関数値の符号の変化が生じない、または、符号変化が生じる区間に対して、探索の間に、NaN、または、Inf 関数が生じるか、または、複素数関数値が生じていることを示します。

[x,fval,exitflag,output] = fzero(...) は、最適化に関する情報を含む構造体 output を出力します。

output.algorithm - 使用したアルゴリズム

output.funcCount - 関数計算の回数

output.iterations - 実行した繰り返し回数

注意このコマンドの目的に対して、零点は、関数が実際に x-軸をクロスする位置で、接する位置ではありません。

引数

fun は、零点が計算される関数です。ベクトル x を入力し、スカラ f を出力します。f は、x で計算される目的関数です。関数 fun は、@ を使って、設定できます。

x = fzero(@myfun,x0)

ここで、myfun は、つぎのような MATLAB 関数です。

function f = myfun(x)
f = ...            % x での関数値の計算

fun は、インラインオブジェクトでも構いません。

x = fzero(inline('sin(x*x)'),x0);

他の引数は、上の表示で記述されたものです。

例題

3の近傍で、サイン関数の零点を検出することで、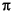を計算しましょう。

x = fzero(@sin,3)
x =
    3.1416

1と2の間で、コサイン関数の零点を求めるには、

x = fzero(@cos,[1 2])
x =

1.5708

cos(1) と cos(2) は、符号が異なることに注意してください。

つぎの関数の零点を求めるには、

f.mと名付けた M-ファイルを書きます。

function y = f(x)
y = x.^3-2*x-5;

2の近傍の零点を求めるには、つぎのようにします。

z = fzero(@f,2)
z =
    2.0946

この関数は、多項式なので、ステートメント roots([1 0 -2 -5]) は、実数と一組の共役複素数を検出します。

    2.0946
   -1.0473 + 1.1359i
   -1.0473 - 1.1359i

アルゴリズム

コマンド fzero は、M-ファイルです。T. Dekker に起源するアルゴリズムは、2分法、セカント(割線)法、逆2次内挿法を組み合わせたものです。いくつかの改良を行った Algol 60 バージョンが、[1] に説明されています。M-ファイル fzero がベースにした Fortran バージョンが、[2] に説明されています。

制限

コマンド fzero は、関数値の符号が変化する点を探索します。関数が連続な場合、これは、関数値がゼロの近傍の点にもなります。関数が連続でない場合、fzero は、零点の代わりに不連続になる点の値を戻す可能性があります。たとえば、fzero(@tan,1) は、 1.5708 を出力します。これは、tan の中の不連続点です。

さらに、コマンド fzero は、関数がx-軸をクロスする点として、零点を定義しています。関数がクロスするのではなく、接する点は、x-軸では、正しい零点ではありません。たとえば、y = x.^2 は、0で、x-軸と接する双曲線です。関数は、x-軸でクロスしないので、零点は求まりません。正しい零点をもった関数に対して、fzero は、Inf、NaN、または、複素数値が検出されるまで、実行し続けます。

参考

roots, fminbnd, function_handle, inline, optimset

参考文献

Brent, R., アルゴリズム for Minimization Without Derivatives, Prentice-Hall, 1973.

Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.

fwrite (serial) gallery