

| MATLAB Release Notes |   |
数学機能
MATLAB 6.5 は、以下の数学機能が追加されています。
これらの機能を以下に示します。この節の最後に、MATLAB数学関数の変更点をまとめた表を示します。
遅延微分方程式
MATLABは、定数遅延をもつ遅延微分方程式(DDEs)を解く機能を提供します。DDEソルバ、dde23は、MATLAB ODEソルバインタフェースと同様のインタフェースを提供し、使いやすいものです。補助関数ddeset, ddeget, devalを使って、問題の解にえいきょうを与える積分プロパティを設定し、dde23で得られる数値解を評価することができます。
詳細は、Initial Value Problems for DDEsとMATLABドキュメントの関数の記述を参照してください。
特異値境界ODE問題
関数bvp4cは、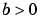 のとき
のとき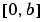 の区間で
の区間で
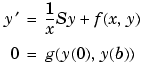
の形式の特異BVPのクラスを解きます。 関数bvpsetは、新規の'SingularTerm'積分プロパティを提供し、これを利用して、定数行列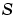 を
をbvp4cに渡すことができます。
詳細は、Solving Singular BVPsとMATLABドキュメントの関数の記述を参照してください。
体積の積分
新規関数triplequadは、3次元長方形領域において、関数 fun(x,y,z) として渡した三重積分を実行します。デフォルトとして、triplequadは求積関数quadを利用して積分を行います。代わりにquadlを選択したり、ユーザ独自の求積関数を使うことができます。
Gamma関数の対数微係数
新規関数psiは、digamma関数としても知られる関数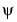 を、配列
を、配列Xの各要素に対して実行します。psiを使って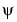 の
のk次微係数を計算したり、Xの要素について他の次数の一連の微係数を計算することができます。
スパース行列LU分解と解法
LU分解とスパース行列の解法は、UMFPACKを利用します。UMFPACKは、Unsymmetric MultiFrontal法を利用して、非対称スパース線形システム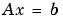 を解くためのルーチンです。これらの行列に対する計算は、かなり速くなります。
を解くためのルーチンです。これらの行列に対する計算は、かなり速くなります。
関数lu. 関数luは、スパース行列に対する2つの新規シンタックスを提供します。これらのシンタックスは、分解に対してUMFPACKを利用します。
シンタックスは、単位下三角行列L、上三角行列U、置換行列PとQを出力します。P*X*Q = L*Uとなります。
\ (バックスラッシュ). 行列の左除算(\)は、正方スパース行列に対してUMFPACKを利用します。
UMFPACKに関する情報は、http://www.cise.ufl.edu/research/sparse/umfpack/からオンラインで入手可能です。UMFPACK Version 4.0 User Guide は、http://www.cise.ufl.edu/research/sparse/umfpack/v4.0/UserGuide.pdfで入手可能です。
行列の数学パフォーマンスの改良
Aが上三角または下三角行列であり、Bがm行n列行列のとき、線形システムAX = Bを解く速度は、最適化 Basic Linear Algebra Subroutines (BLAS)の利用により改良されています。最適化BLASは、Automatically Tuned Linear Algebra Software (ATLAS)で提供されます。
BLASは、行列*ベクトル、ベクトル*行列、行ベクトル*列ベクトルのような行列の乗算のパフォーマンスを改良するためにも用いられます。
ATLAS BLASは、WindowsおよびLinux双方のオペレーティングシステムにおいて、Pentium 4 に対してはじめて適用され、線形代数コア関数の速度を改良しています。
キャッシュをより適切に利用することにより、行列の転置の速度はすべての行列に対して増加していますが、特にサイズが2のベキ乗である行列に対して増加しています。
新規関数のまとめ
| 関数 |
目的 |
|
定数遅延をもつ遅延微分方程式(DDEs)の初期値問題を解く |
|
ddesetにより作成されたオプション醸造体からプロパティを取得 |
|
ソルバ積分プロパティを含むDDEオプション構造体の作成/変更 |
|
Psi (polygamma)関数(gamma関数の対数微係数) |
|
三重積分の数値評価 |
変更された関数のまとめ
| 関数 |
機能強化されたあるいは変更された点 |
|
|
新規オプション'SingularTerm'を使って、特異なBVPの特異項として行列を指定することができます。このオプションは、以下の形式の方程式に対して定数行列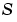 を指定します。 を指定します。 | |
|
3つの新規シンタックスを提供します。[R,P] = corrcoef(...)は、非相関の仮説の検証に対するp値からなる行列であるPを出力します。
| |
|
dde23からの出力も受け取ります。 | |
|
house |
新規シンタックス |
|
leslie |
gallery('leslie',a,b)は、平均の出生数a(1:n)と生存率b(1:n-1)をもつn行n列のLeslie行列を出力します。 |
|
orthog |
gallery('orthog',n,k)は、行列の新規タイプkを追加しています。k = 6 は、Q(i,j) = sqrt(2/n)*cos((i-1/2)*(j-1/2)*pi/n)のように、離散余弦変換として生じた対称行列を指定します。 |
|
randsvd |
大きい次元に対して、新規引数methodを使って、(より多くのflopsを利用しても)大きい次元に対してより高速な方法を指定することができます。 |
|
新規シンタックスlegendre(n,X,'norm')は、正規化随伴Lengendre関数を計算します。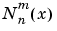 | |
|
新規シンタックス[x,flag,relres,iter,resvec,lsvec] = lsqr(...)は、各繰り返しでのスケーリングされた標準の残差を推定してベクトルlsvecに出力します。 | |
lu |
UMFPACKを使って、スパース行列の分解の速度を改良したり、スパース行列に対して2つのシンタックスを追加します。[L,U,P,Q] = lu(X)[L,U,P,Q] = lu(X,thresh)新規出力 Qは、スパースな場合の空きを削減するため利用される列転置行列です。Pは、数値安定性を目的として利用される行転置行列です。UNFPACKに関する詳細は、スパース行列LU分解と解法を参照してください。 | |
qrdelete |
これらの関数の2つの新規シンタックスは、QR分解での行および列の削除ならびに挿入に対して提供されます。[Q1,R1] = qrdelete(Q,R,j,'col')[Q1,R1] = qrdelete(Q,R,j,'row')[Q1,R1] = qrinsert(Q,R,j,x,'col')[Q1,R1] = qrinsert(Q,R,j,x,'row')オリジナルのシンタックスqrdelete(Q,R,j)およびqrinsert(Q,R,j,x)のデフォルトは、 'col'です。 | |
/ (スラッシュ) |
正方スパース行列の左除算および右除算に対してはUMFPACKを利用します。 | |
/ (スラッシュ) |
左(\)または右(/)除算を使った、特異な下三角または上三角行列のその他の行列による除算の結果は、変更されている場合があります。従来は、rcond(A) = 0である特異な正方行列Aに対して、毛かkあh常にInfの行列でした。この変更は、上記のパフォーマンスの改良の結果です。例題は、Mathematics Upgrade Issuesを参照してください。 | |
 | 開発環境の機能 | プログラミングとデータタイプの機能 |  |