MATLAB Function Reference

legendre

随伴 Legendre 関数

表示

P = legendre(n,X)
S = legendre(n,X,'sch')

定義

Legendre 関数は、つぎのように定義されます。

ここで、

は、n 次の Legendre 多項式です。

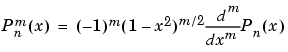
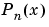
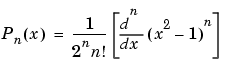
Schmidt 準正規化随伴 Legendre 関数は、つぎの式により非正規化随伴 Legendre 関数 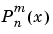と対応付けられます。

ここで、m > 0。

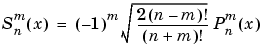
詳細

P = legendre(n,X) は、X で求められる位数 n で、次数 m = 0,1,...,n の Legendre関数を計算します。引数 n は、256 以下のスカラの整数で、X は定義域 -1 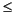x 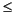1の実数値を含まなければいけません。

出力された配列 P は、X よりも1つ大きい次元をもち、各要素 P(m+1,d1,d2...) は、X(d1,d2...)で 求められる位数 n で、次数 m の随伴Legendre関数をもちます。

X がベクトルの場合ば、P は、つぎの型の行列です。

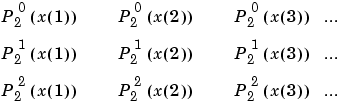
S = legendre(...,'sch') は、Schmidt 準正規化随伴 Legendre 関数 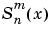を計算します。

例題

legendre(2,0:0.1:0.2) は、つぎの行列を出力します。

	x = 0	x = 0.1	x = 0.2
m = 0	-0.5000	-0.4850	-0.4400
m = 1	0	-0.2985	-0.5879
m = 2	3.0000	2.9700	2.8800

この行列は、上の式に示した型であることに注意してください。

つぎのように与えると

X = rand(2,4,5); N = 2;
P = legendre(N,X) 

は、3*2*4*5で、P(:,1,2,3) は 、legendre(n,X(1,2,3)) と同じです。

legend

length