hinf, dhinf, linf (Robust Control Toolbox)

Robust Control Toolbox

hinf, dhinf, linf

H optimal control synthesis (continuous and discrete)

Syntax

linf 
    Inputs: A, B1, B2, C1, C2, D11, D12, D21, D22 
    Outputs: acp, bcp, ccp, dcp, acl, bcl, ccl, dcl 
[acp,,acl,,hinfo,ak,,dk22] = (d)hinf(A,,D22)
[acp,,acl,,hinfo,ak,,dk22] = (d)hinf(A,,D22,au,,du)
[acp,,acl,,hinfo,ak,,dk22] = ... (d)hinf(A,,D22,au,,du,verbose)
[sscp,sscl,hinfo,tssk] = (d)hinf(TSSP) 
[sscp,sscl,hinfo,tssk] = (d)hinf(TSSP,ssu,)
[sscp,sscl,hinfo,tssk] = (d)hinf(TSSP,ssu,verbose)

Description
linf and hinf solve the small-gain infinity-norm robust control problem; i.e., find a stabilizing controller F(s) for a system

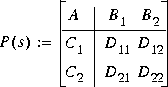
such that the closed-loop transfer function satisfies the infinity-norm inequality

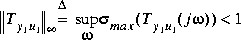
Figure 1-7: Particular F(s)

State-space matrices for a particular solution F(s) and the corresponding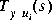

are returned as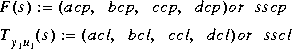

linf finds the solution F(s) using the Hankel approximation algorithm outlined in [15], whereas hinf uses a more recent two-Riccati algorithm [18, 8, 9, 3, 5, 6, 17].

In general, the solution to the infinity-norm optimal control problem is non-unique. Whereas linf computes only a particular F(s), hinf computes in addition the all- solution controller parameterization K(s) such that all solutions to the infinity-norm control problem are parameterized by a free stable contraction map U(s) constrained by 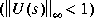(see Figure 1-8). By default hinf will set U(s) = 0, if no U(s) is supplied. But if you specify

U(s) := (au, bu, cu, du) in advance, hinf will compute the corresponding F(s) as shown in Figure 1-8.

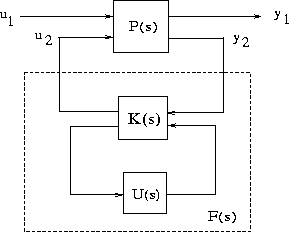
Figure 1-8: All-solution F(s)

An important use of the infinity-norm control theory is for direct shaping of closed-loop singular value Bode plots of control systems. In such cases, the system P(s) will typically be the plant augmented with suitable loop-shaping filters -- see augss and augtf.

dhinf solves the discrete counterpart of the problem using bilinear transform bilin, since the infinity norm of a given discrete problem is preserved under such a transformation in the continuous domain. The resulting continuous H controller is then transformed back to the discrete domain via the inverse bilinear transform inside program dhinf. The discrete time H theory is documented nicely in [10].

Examples
See the Tutorial chapter for H design examples and their demonstrations in rctdemo. Also see the examples in hinfopt.

Algorithm
linf implements the first generation state-space H theory developed in 1984 to 1987 ([2, 14, 1, 4]), which splits the H problem into three phases:

1: Plant augmentation (see augtf, augss).

2: Youla parametrization (see youla).

3: Interpolation via optimal anticausal descriptor Hankel approximation (see ohklmr).

The bottleneck of linf algorithm is the lengthy model reduction work required in step 3. However, successful results using linf have been reported in [12, 16].

The 2-Riccati H controller has been derived via two distinct approaches -- game theory (in time domain) and all-pass embedding (in frequency domain). The game theory approach is conceptually abstract but leads to a much simpler derivation. In 1977 Mageirou and Ho [11] solved the full-state feedback case via game theory and others [7] later "rediscovered" it. Subsequently, Doyle et al.[3] extended the full-state feedback result into its observer dual and established a separation principle for H (a counterpart of the LQG). A frequency domain derivation for the dynamical output feedback case was initiated by Limebeer, et al. [8, 9, 6] using Parrott's all-pass embedding technique and the optimal Hankel norm theorem. Both approaches require a large effort and much algebraic manipulation to handle all but very special cases in which the plant "C" and "D" matrices satisfied certain conditions. Safonov et al. [17] developed a loop-shifting technique to simplify the derivations, introduced a descriptor matrix-pencil representation and improved existence conditions. The latter eliminated numerical instabilities that had plagued previous formulations of the H control theory. A matrix pencil is an s-dependent matrix of the form As + B. The generalized eigenvalues of a regular square matrix pencil, denoted 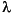i(As + B), are the values of 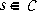at which the determinant of the pencil vanishes; numerically robust algorithms exist for computing the generalized eigenvalues and associated eigenspaces.

hinf implements the loop-shifting "two-Riccati" formulae for the infinity-norm control [17]. The chief advantage of hinf over linf is that the lengthy numerically sensitive model reduction work is completely eliminated. Instead, hinf produces an H controller with the same state dimension as the augmented plant P(s).

Limitations
In contrast to the H² problem, a solution to the infinity-norm control problem does not exist for every P(s). Error messages such as "Riccati solver fails" are possible indications that the augmented system P(s) arises from singular-value Bode plot specifications that are infeasible or, possibly, that certain other well-posedness conditions have been violated. In particular, the algorithms linf and hinf require that the following conditions hold: [13]

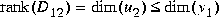
that is, D₁₂must be a "tall" matrix with full "column" rank.

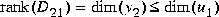
that is, D₂₁must be a "fat" matrix with full "row" rank.

Careful problem formulations can avoid some numerically or physically ill-posed H problems. For example,

1: Always include a proper control weighting W₂ to ensure that D₁₂is a full column rank (ref. augtf)

2: Form a standard mix-sensitivity problem with D₂₁ square. This formulation has solved a lot of real world control problems (flight control, large space structure, spacecraft attitude control, etc.).

3: Use some classical loop-shaping judgments to penalize your physical variables.

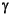4: If still no solution is found, try -Iteration hinfopt on the problem.

If you have exhausted all the above possibilities, you can always call the authors for help.

See Also
augss, augtf, h2lqg, hinfdemo, linfdemo, lqg, ltru, ltry

References
[1] R. Y. Chiang and M. G. Safonov, "The LINF Computer Program for L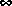 Controller Design," USC report EECG-0785-1, ver. 1.0 2.0, July, 1986 and 1987.

[2] J. Doyle, Advances in Multivariable Control. Lecture Notes at ONR/Honeywell Workshop. Minneapolis, MN, Oct. 8-10, 1984.

[3] J. Doyle, K. Glover, P. Khargonekar, and B. Francis, "State-space solutions to standard H² and H control problems," IEEE Trans. Automat. Contr., AC-34, no. 8, pp. 831-847, Aug. 1989.

[4] B. A. Francis, A Course in H Control Theory, Springer-Verlag: 1987.

[5] K. Glover and J. C. Doyle, "State Space Formulae for All Stabilizing Controllers that Satisfy an H-Norm Bound and Relations to Risk Sensitivity", Systems and Control Letters, 1988.

[6] K. Glover, D. J. N. Limebeer, J. C. Doyle, E. M. Kasenally and M. G. Safonov, "A Characterization of All Solutions to the Four Block General Distance Problem", SIAM J. Control and Opt., vol. 27, pp. 283-324, 1991.

[7] P. P. Khargonekar, I. R. Petersen, and M. A. Rotea, "H optimal control with state feedback," IEEE Trans. Automat. Contr., AC-33, pp. 783-786, 1988.

[8] D.J.N. Limebeer and E. Kasenally, unpublished notes, 1987.

[9] D.J.N. Limebeer, E. M. Kasenally, E. Jaimouka, and M. G. Safonov, "A Characterization of All Solutions to the Four Block General Distance Problem," Proc. 27th IEEE Conf. Decision Contr., Austin, TX, 1988.

[10] D.J.N. Limebeer, M. Green, and D. Walker, "Discrete Time H control," Proc. of Conf. on Decision and Control, Tampa, FL., Dec. 1989.

[11] E. F. Mageirou and Y. C. Ho, "Decentralized Stabilization via Game Theoretic Methods," Automatica, vol. 13, pp. 393-399, 1977.

[12] M. G. Safonov and R. Y. Chiang, "CACSD Using the State-Space L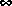 Theory -- A Design Example", Proc. IEEE Conf. on CACSD, Washington D. C., Sep. 24-26, 1986, also IEEE Trans. on Automat. Contr., AC-33, No. 5, pp. 477-479, May 1988.

[13]M. G. Safonov, "Imaginary-Axis Zeros in Multivariable HOptimal Control", in R. F. Curtain (editor), Modelling, Robustness and Sensitivity Reduction in Control Systems, pp. 71-81, Springer-Verlag, Berlin, 1987. Proc. NATO Advanced Research Workshop on Modeling, Robustness and Sensitivity Reduction in Control Systems, Groningen, The Netherlands, Dec. 1-5, 1986.

[14] M. G. Safonov, E. A. Jonckheere, M. Verma and D. J. N. Limebeer, "Synthesis of Positive Real Multivariable Feedback Systems", Int. J. Control, vol. 45, no. 3, pp. 817-842, 1987.

[15] M. G. Safonov, R. Y. Chiang, and D. J. N. Limebeer, "Hankel Model Reduction without Balancing - A Descriptor Approach," Proc. IEEE Conf. on Decision and Control, Los Angeles, CA, Dec. 9-11, 1987.

[16] M. G. Safonov, R. Y. Chiang and H. Flashner, "H Control Synthesis for a Large Space Structure," AIAA J. Guidance, Control and Dynamics, 14, 3, pp. 513-520, May/June 1991.

[17] M. G. Safonov, D. J. N. Limebeer and R. Y. Chiang, "Simplifying the H Theory via Loop Shifting, Matrix Pencil and Descriptor Concepts", Int. J. Contr., vol. 50, no. 6, pp. 2467-2488, 1989.

[18] G. Stein, Lecture Notes, Tutorial Workshop on H Control Theory, Los Angeles, CA, Dec. 7-8, 1987.

h2lqg, dh2lqg hinfopt