| Robust Control Toolbox | |
State-space or transfer function plant augmentation for use in weighted mixed-sensitivity H
and H2 design.
Syntax
[a,b1,b2,c1,c2,d11,d12,d21,d22] = ... augss(ag,bg,,aw1,bw1,,aw2,bw2,,aw3,bw3,) [a,b1,b2,c1,c2,d11,d12,d21,d22] = ... augss(ag,bg,,aw1,bw1,,aw2,bw2,,aw3,bw3,,w3poly) [a,b1,b2,c1,c2,d11,d12,d21,d22] = ... augtf(ag,bg,cg,dg,w1,w2,w3) [tss] = augss(ssg,ssw1,ssw2,ssw3,w3poly) [tss] = augtf(ssg,w1,w2,w3) [tss] = augss(ssg,ssw1,ssw2,ssw3)
augss computes a state-space model of an augmented plant P(s) with weighting functions W1(s), W2(s), and W3(s) penalizing the error signal, control signal and output signal respectively (see block diagram) so that the closed-loop transfer function matrix is the weighted mixed sensitivity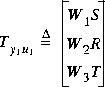
.
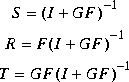Figure 1-2: Plant Augmentation.
The transfer functions G(s), W1(s) and W3(s)G(s) must be proper, i.e., bounded as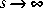
. However, W3(s) may be improper. Input data of 
augss are the state-space system matrices of G(s), W1(s), W2(s)and W3(s):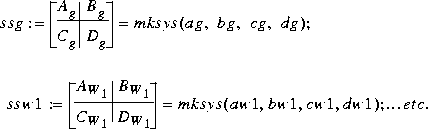
The possibly improper transfer function matrix
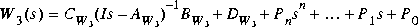
If one of the weighting functions is absent, e.g., W2(s) = 0, then simply assign ssw2 = [ ].
augtf does the plant augmentation as well, except the weighting functions W1, W2 and W3 are input as diagonal transfer function matrices. The numerator and denominator of each diagonal entry of the transfer functions are entered as rows of the weighting matrix. For example, the weightings
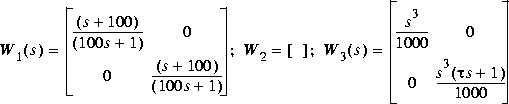
used in the Hfighter design presented in the Tutorial chapter are entered as
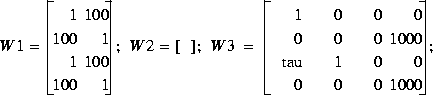
Algorithm
The augmented plant P(s) produced by augss is
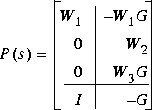
augtf calls augss internally after a series of transfer function to state-space transformations on W1, W2, and W3.
Limitations
Note that if the augmented plant is to be used for H synthesis via hinf or linf, then it is essential that the weights W1, W2, and W3 be selected so that the augmented plant has a "D12" matrix of full column rank. An easy way to ensure that this is the case is to choose a W2(s) with an invertible "D-matrix", e.g.,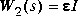 
where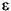 
is any non-zero number.
See Also
h2lqg, hinf, hinfdemo, linf, linfdemo, dh2lqg, dhinf
| augd | balmr, schmr | |
