h2lqg, dh2lqg (Robust Control Toolbox)

Robust Control Toolbox

h2lqg, dh2lqg

H² optimal control synthesis (continuous and discrete).

Syntax

[acp,bcp,ccp,dcp,acl,bcl,ccl,dcl] = (d)h2lqg(A,B1,B2,,D22) 
[acp,bcp,ccp,dcp,acl,bcl,ccl,dcl] = (d)h2lqg(A,B1,B2,,D22,aretype) 
[sscp,sscl] = (d)h2lqg(TSS)
[sscp,sscl] = (d)h2lqg(TSS,aretype)

Description
h2lqg solves H² optimal control problem; i.e., find a stabilizing positive-feedback controller for an "augmented" system

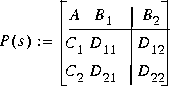
such that the H²-norm of the closed-loop transfer function matrix 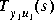is minimized:

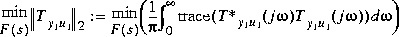
The stabilizing feedback law F(s) and the closed-loop transfer function 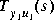are returned 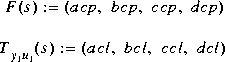as

Figure 1-6: H2 Control Synthesis.

The optional input aretype determines the method used by ARE solver aresolv. It can be either "eigen" (default), or "Schur".

dh2lqg solves the discrete counterpart of the problem by directly forming two discrete ARE's and solve them via daresolv. Note that in contrast to the H case, the bilinear transform technique does not apply in the H² case. This is because the H² norm, unlike the H norm, is not invariant under bilinear transformation.

Examples
See the Tutorial chapter for design examples and demonstrations. Especially, see the comparison between H² synthesis and Hsynthesis in the Fighter H²and HDesign Example in the Tutorial section.

Algorithm
H2lqg solves the H²-norm optimal control problem by observing that it is equivalent to a conventional Linear-Quadratic Gaussian optimal control problem involving cost

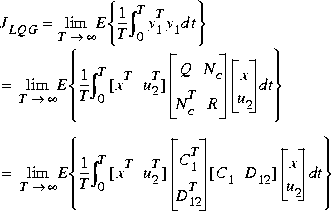
with correlated white plant noise and white measurement noise entering the system via the channel [B₁ D₂₁]T and having joint correlation function

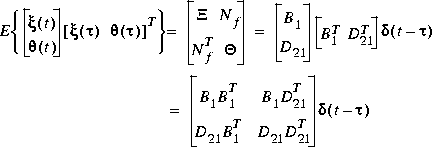
The H² optimal controller F(s) is thus realizable in the usual LQG manner as a full-state feedback K_c and a Kalman filter with residual gain matrix K_f.

1: Kalman Filter

where

Tand satisfies ARE

2: Full-State Feedback

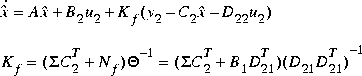
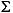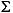where P = PT and satisfies ARE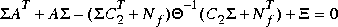

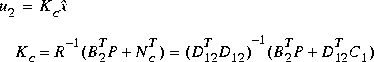
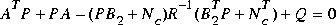
The final positive-feedback H²optimal controller 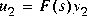has a familiar closed-form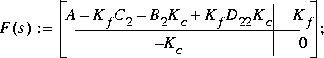

It can be easily shown that by letting 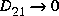the H²-optimal LQG problem is essentially equivalent to LQ full-state feedback loop transfer recovery (see ltru). Dually, as 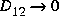you obtain Kalman filter loop transfer recovery [1] (see ltry).

Limitations

1: (A, B₂, C₂) must be stabilizable and detectable.

2: D₁₁ must be zero, otherwise the H² optimal control problem is ill-posed. If a nonzero D₁₁ is given, the algorithm ignores it and computes the H²optimal control as if D₁₁ were zero.

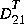3: D₁₂ and must both have full column rank.

See Also

hinf, dhinf, lqg, ltru, ltry, aresolv, daresolv

References
[1] J. Doyle and G. Stein, "Multivariable Feedback Design: Concepts for a Classical/Modern Synthesis," IEEE Trans. on Automat. Contr., AC-26, pp. 4-16, 1981.

[2] J. Doyle, Advances in Multivariable Control. Lecture Notes at ONR/Honeywell Workshop. Minneapolis, MN, Oct. 8-10, 1984.

[3] M. G. Safonov, A. J. Laub, and G. Hartmann, "Feedback Properties of Multivariable Systems: The Role and Use of Return Difference Matrix," IEEE Trans. of Automat. Contr., AC-26, pp. 47-65, 1981.

[4] G. Stein and M. Athans, "The LQG/LTR Procedure for Multivariable Feedback Control Design," IEEE Trans. on Automat. Contr., AC-32, pp. 105-114, 1987.

graft hinf, dhinf, linf