| Robust Control Toolbox | |
LQG optimal control synthesis.
Syntax
Description
lqg computes an optimal computes an optimal controller to stabilize the plant G(s)
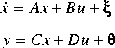
and minimize the quadratic cost function
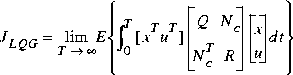
Figure 1-12: LQG Synthesis.
The plant noise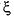
and measurement noise 
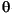are white and Gaussian with joint correlation function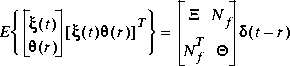
The input variables W and V are
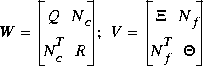
The LQG controller is returned as F(s) := (af, bf, cf, df).
Algorithm
The solution of the LQG problem is a combination of the solutions of Kalman filtering and full-state feedback problems based on the so-called separation principle. The individual problems are explained under lqe and lqr in the Control System Toolbox. The final negative-feedback controller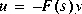 
has the form (e.g. [1])
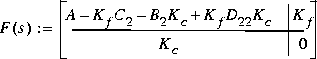
Note that the sign of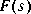 
is minus that in the function h2lqg; this is because by convention lqg feedback is negative (i.e,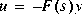 
) while the h2lqg is positive (i.e,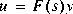 
). The lqg feedback can also be realized as a full-state feedback and Kalman filter:
See Also
h2lqg, hinf, hinfdemo, linf, linfdemo, ltru, ltry
References
[1] M. Athans, "The Role and Use of the Stochastic Linear-Quadratic-Gaussian Problem in Control System Design," IEEE Trans. Automat. Contr., AC-16, pp. 529-552, Dec. 1971.
| lftf | ltru, ltry | |
