Prismatic (SimMechanics)

Represent a prismatic joint with one translational degree of freedom

Library

Joints

Description

The Prismatic block represents a single translational degree of freedom (DoF) along a specified axis between two bodies. A prismatic joint is one of SimMechanics primitive joints, along with revolute and spherical.

The Prismatic block is assembled: you must connect each side of the Joint block to a Body block at a Body coordinate system (CS) point, and the origins of these Body CSs must lie along the prismatic axis, to within assembly tolerances. These Body CS origins do not need to be collocated in space.

You can connect any Joint block to two and only two Body blocks, and Joints have a default of two Connector Ports for connecting to base and follower Bodies.

A Joint block represents only the abstract relative motion of two bodies, not the bodies themselves. You must specify a reference CS to define the direction of the joint axis.

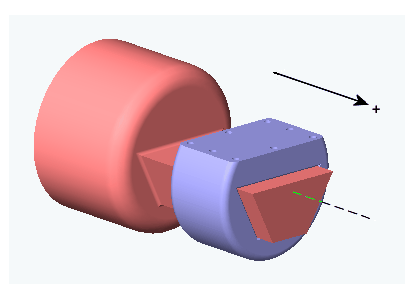
Prismatic motion of follower (blue) relative to base (red)

Dialog Box and Parameters

The dialog box has two active areas, Connection parameters and Parameters.

Connection Parameters

Current base: When you connect the base (B) Connector Port on the Prismatic block to a Body CS Port on a Body, this parameter is automatically reset to the name of this Body CS. See the following Prismatic base and follower Body Connector Ports figure.
Current follower: When you connect the follower (F) Connector Port on the Prismatic block to a Body CS Port on a Body, this parameter is automatically reset to the name of this Body CS. See the following Prismatic base and follower Body Connector Ports figure.
Number of sensor/actuator ports: Using this spinner menu, you can set the number of extra Connector Ports needed for connecting Joint Actuator and Joint Sensor blocks to this Joint. The default is 0.; The motion of a Prismatic is specified in linear units.

The base (B)-follower (F) Body sequence determines the sense of positive motion. Positive translation is the follower moving in the direction of the translation axis.

Prismatic base and follower Body Connector Ports

Parameters

Toggle between the Axes and Advanced panels with the tabs.

The entries on the Axes pane are required. They specify the direction of the translational DoF that the Prismatic represents.

Name: This column automatically displays the name of each primitive joint contained in the Joint block. For Prismatic, there is only one primitive joint, a prismatic, labeled P1.
Primitive: This column automatically displays the type of each primitive joint contained in the Joint block. For Prismatic, there is only one primitive type, labeled Prismatic.
Axis of translation [x y z]: Enter here as a three-component vector the directional axis along which this translational DoF can move. The default vector is [0 0 1]. The axis is a directed vector whose overall sign matters.
Reference csys: Using the pull-down menu, choose the coordinate system (World, the base Body CS, or the follower Body CS) whose coordinate axes the vector axis of translation is oriented with respect to. This CS also determines the absolute meaning of force and motion along the joint axis. The default is WORLD.

The Advanced pane is optional. You use it to control the way SimMechanics interprets the topology of your schematic diagram.

Mark as the preferred cut joint: In a closed loop, one and only one joint is cut during the simulation. SimMechanics does the cutting internally and automatically.; If you want this particular joint to be weighted preferentially for cutting during the simulation, select the check box. The default is unselected.

See Modeling Joints for more on representing DoFs with Joints.

See Checking Schematic Topology and How SimMechanics Works for more on closed loops and cutting.

Point-Curve Constraint Revolute