Partial Differential Equation Toolbox

Examples of Elliptic Problems

This section describes the solution of some elliptic PDE problems. The last problem, a minimal surface problem, is nonlinear and illustrates the use of the nonlinear solver. The problems are solved using both the graphical user interface and the command-line functions of the PDE Toolbox. The topics in include

• Poisson's Equation on Unit Disk
• A Scattering Problem
• A Minimal Surface Problem
• Domain Decomposition

Poisson's Equation on Unit Disk

As a first example of an elliptic problem, let us use the simplest elliptic PDE of all -- Poisson's equation.

The problem formulation is

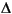-U = 1 in 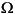, U = 0 on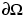

where 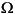is the unit disk. In this case, the exact solution is

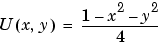
so the error of the numeric solution can be evaluated for different meshes.

Using the Graphical User Interface

With the pdetool graphical user interface (GUI) started, perform the following steps using the Generic Scalar mode:

1. Using some of the Option menu features, add a grid and turn on the "snap-to-grid" feature. Draw a circle by clicking the button with the ellipse icon with the + sign, and then click-and-drag from the origin, using the right mouse button, to a point at the circle's perimeter. If the circle that you create is not a perfect unit circle, double-click the circle. This opens a dialog box where you can specify the exact center location and radius of the circle.
2. Enter the Boundary mode by clicking the button with the icon. The boundaries of the decomposed geometry are plotted, and the outer boundaries are assigned a default boundary condition (Dirichlet boundary condition, u = 0 on the boundary). In this case, this is what we want. If the boundary condition is different, double-click the boundary to open a dialog box through which you can enter and display the boundary condition.
3. To define the partial differential equation, click the PDE button. This opens a dialog box, where you can define the PDE coefficients c, a, and f. In this simple case, they are all constants: c = 1, f = 1, and a = 0.
4. Click the button or select Initialize Mesh from the Mesh menu. This initializes and displays a triangular mesh.
5. Click the Refine button or select Refine Mesh from the Mesh menu. This causes a refinement of the initial mesh, and the new mesh is displayed.
6. To solve the system, just click the = button. The toolbox assembles the PDE problem and solves the linear system. It also provides a plot of the solution. Using the Plot Selection dialog box, you can select different types of solution plots.

   

7. To compare the numerical solution to the exact solution, select the user entry in the Property pop-up menu for Color in the Plot Selection dialog box. Then input the MATLAB expression u-(1-x.^2-y.^2)/4 in the user entry edit field. You obtain a plot of the absolute error in the solution.

You can also compare the numerical solution to the exact solution by entering some simple command-line-oriented commands (see the next section). It is easy to export the mesh data and the solution to the MATLAB main workspace by using the Export . . . options from the Mesh and Solve menus. To refine the mesh and solve the PDE successively, simply click the refine and = buttons until the desired accuracy is achieved. (Another possibility is to use the adaptive solver.)

Using Command-Line Functions

First you must create a MATLAB function that parameterizes the 2-D geometry -- in this case a unit circle.

The M-file circleg.m returns the coordinates of points on the unit circle's boundary. The file conforms to the file format described on the reference page for pdegeom. You can display the M-file by typing type circleg.

Also, you need a function that describes the boundary condition. This is a Dirichlet boundary condition where u = 0 on the boundary. The M-file circleb1.m provides the boundary condition. The file conforms to the file format described on the reference page for pdebound. You can display the M-file by typing type circleb1.

Now you can start working from the MATLAB command line:

• [p,e,t]=initmesh('circleg','Hmax',1); 
  error=[]; err=1; 
  while err > 0.001, 
      [p,e,t]=refinemesh('circleg',p,e,t); 
      u=assempde('circleb1',p,e,t,1,0,1); 
      exact=-(p(1,:).^2+p(2,:).^2-1)/4; 
      err=norm(u-exact',inf); 
      error=[error err]; 
     end 
  pdemesh(p,e,t) 
  pdesurf(p,t,u) 
  pdesurf(p,t,u-exact')
  

The first MATLAB command creates the initial mesh using the parameterizing function circleg.

Also, initialize a vector error for the maximum norm errors of the successive solutions and set the initial error err to 1. The loop then runs until the error of the solution is smaller than 10^-3.

1. Refine the mesh. The current triangular mesh, defined by the geometry circleg, the point matrix p, the edge matrix e, and the triangle matrix t, is refined, and the mesh is returned using the same matrix variables.
2. Assemble and solve the linear system. Note that the coefficients of the elliptic PDE are constants (c = f = 1, a = 0) for this simple case. circleb1 contains a description of the boundary conditions, and p, e, and t define the triangular mesh.
3. Find the error of the numerical solution produced by the PDE Toolbox. The vector exact contains the exact solution at the nodes. Note that what you actually find is the max-norm error of the solution at the nodes.
4. Plot the mesh, the solution, and the error. Notice that the plot function pdesurf as third argument can take any vector of values on the mesh given by p and t, not just the solution. In this case you are also plotting the error function.
   
   

The Error Function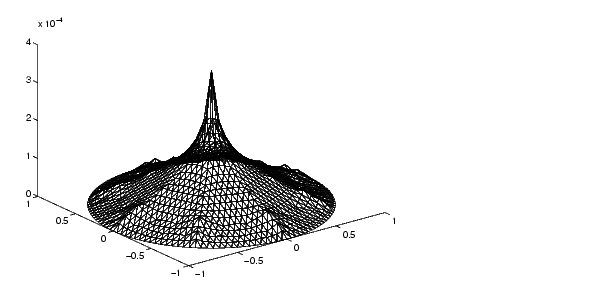

pdedemo1 performs all the above steps.

Examples

A Scattering Problem