Partial Differential Equation Toolbox

A Scattering Problem

The scattering problem is to compute the waves reflected from an object illuminated by incident waves. For this problem consider an infinite horizontal membrane subjected to small vertical displacements U. The membrane is fixed at the object boundary.

We assume that the medium is homogeneous so that the wave speed is constant, c.

Note    Do not confuse this c with the parameter c appearing in the PDE Toolbox.

When the illumination is harmonic in time, we can compute the field by solving a single steady problem. With U(x,y,t) = u(x,y)e-i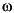t, the wave equation

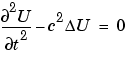
turns into -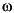 2u - c2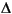u= 0 or the Helmholtz's equation

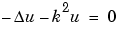
where k, the wave number, is related to the angular frequency 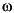, the frequency f, and the wavelength 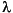by

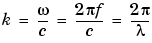
We have yet to specify the boundary conditions. Let the incident wave be a plane wave traveling in the direction 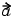= (cos(a),sin(a))

where

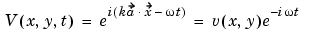
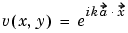
u is the sum of v and the reflected wave r,

u = v + r

The boundary condition for the object's boundary is easy: u = 0, i.e.,

r = -v(x,y)

For acoustic waves, where v is the pressure disturbance, the proper condition would be

• .

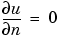The reflected wave r travels outward from the object. The condition at the outer computational boundary should be chosen to allow waves to pass without reflection. Such conditions are usually called nonreflecting, and we use the classical Sommerfeld radiation condition. As 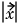approaches infinity, r approximately satisfies the one-way wave equation

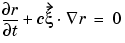
which allows waves moving in the positive 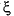-direction only ( 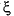is the radial distance from the object). With the time-harmonic solution, this turns into the generalized Neumann boundary condition

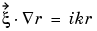
For simplicity, let us make the outward normal of the computational domain approximate the outward 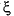-direction.

Using the Graphical User Interface

You can now use pdetool to solve this scattering problem. Using the Generic Scalar mode, start by drawing the 2-D geometry of the problem. Let the illuminated object be a square SQ1 with a side of 0.1 units and center in [0.8 0.5] and rotated 45 degrees, and let the computational domain be a circle C1 with a radius of 0.45 units and the same center location. The Constructive Solid Geometry (CSG) model is then given by C1-SQ1.

For the outer boundary (the circle perimeter), the boundary condition is a generalized Neumann condition with q = -ik. The wave number k = 60, which corresponds to a wavelength of about 0.1 units, so enter -60i as a constant q and 0 as a constant g.

For the square object's boundary, you have a Dirichlet boundary condition:

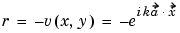
In this problem, the incident wave is traveling in the -x direction, so the boundary condition is simply

r = -e-ikx

Enter this boundary condition in the Boundary Condition dialog box as a Dirichlet condition: h=1, r=-exp(-i*60*x). The real part of this is a sinusoid.

For sufficient accuracy, about 10 finite elements per wavelength are needed. The outer boundary should be located a few object diameters from the object itself. An initial mesh generation and two successive mesh refinements give approximately the desired resolution.

Although originally a wave equation, the transformation into a Helmholtz's equation makes it -- in the PDE Toolbox context, but not strictly mathematically -- an elliptic equation. The elliptic PDE coefficients for this problem are c = 1, a = -k2 = -3600, and f = 0. Open the PDE Specification dialog box and enter these values.

The problem can now be solved, and the solution is complex. For a complex solution, the real part is plotted and a warning message is issued.

The propagation of the reflected waves is computed as

Re(r(x,y)e-it)

which is the reflex of

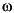To see the whole field, plot

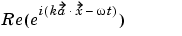
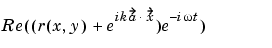
The reflected waves and the "shadow" behind the object are clearly visible when you plot the reflected wave.

To make an animation of the reflected wave, the solution and the mesh data must first be exported to the main workspace. Then make a script M-file or type the following commands at the MATLAB prompt:

• h=newplot; hf=get(h,'Parent'); set(hf,'Renderer','zbuffer')
  axis tight, set(gca,'DataAspectRatio',[1 1 1]); axis off 
  M=moviein(10,hf); 
  maxu=max(abs(u)); 
  colormap(cool) 
  or j=1:10, 
     ur=real(exp(-j*2*pi/10*sqrt(-1))*u)); 
     pdeplot(p,e,t,'xydata',ur,'colorbar','off','mesh','off'); 
     caxis([-maxu maxu]); 
     axis tight, set(gca,'DataAspectRatio',[1 1 1]); axis off 
     M(:,j)=getframe; 
   end
  movie(hf,M,50);
  

pdedemo2 contains a full command-line demonstration of the scattering problem.

Examples of Elliptic Problems

A Minimal Surface Problem