Partial Differential Equation Toolbox

A Minimal Surface Problem

In many problems the coefficients c, a, and f do not only depend on x and y, but also on the solution u itself. Consider the equation

on the unit disk

with on .

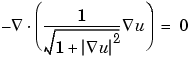
This problem is nonlinear and cannot be solved with the regular elliptic solver. Instead, the nonlinear solver pdenonlin is used.

Let us solve this minimal surface problem using the pdetool GUI and command-line functions.

Using the Graphical User Interface

Make sure that the application mode in the pdetool GUI is set to Generic Scalar. The problem domain is simply a unit circle. Draw it and move to the Boundary mode to define the boundary conditions. Use Select All from the Edit menu to select all boundaries. Then double-click a boundary to open the Boundary Condition dialog box. The Dirichlet condition u = x2 is entered by typing x.^2 into the r edit box. Next, open the PDE Specification dialog box to define the PDE. This is an elliptic equation with

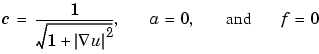
The nonlinear c is entered into the c edit box as

• 1./sqrt(1+ux.^2+uy.^2)
  

Initialize a mesh and refine it once.

Before solving the PDE, select Parameters . . . from the Solve menu and check the Use nonlinear solver option. Also, set the tolerance parameter to 0.001.

Click the = button to solve the PDE. Use the Plot Selection dialog box to plot the solution in 3-D (check u and continuous selections in the Height column) to visualize the saddle shape of the solution.

Using Command-Line Functions

Working from the command line, the following sequence of commands solves the minimal surface problem and plots the solution. The M-files circleg and circleb2 contain the geometry specification and boundary condition functions, respectively.

• g='circleg';
  b='circleb2'; 
  c='1./sqrt(1+ux.^2+uy.^2)'; 
  rtol=1e-3; 
  
  [p,e,t]=initmesh(g); 
  [p,e,t]=refinemesh(g,p,e,t); 
  
  u=pdenonlin(b,p,e,t,c,0,0,'Tol',rtol); 
  
  pdesurf(p,t,u)
  

You can run this example by typing pdedemo3.

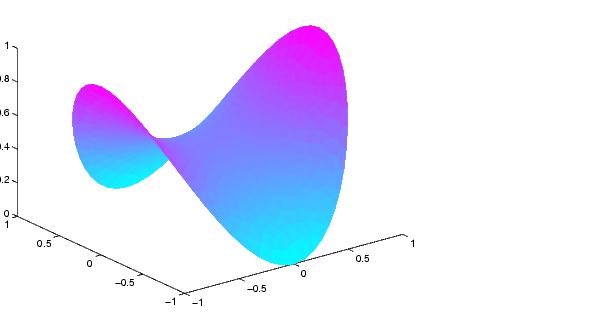
A Scattering Problem

Domain Decomposition