Partial Differential Equation Toolbox

pdegeom

Geometry M-file

Syntax

• ne=pdegeom 
  d=pdegeom(bs) 
  [x,y]=pdegeom(bs,s)
  

Description

We represent 2-D regions by parameterized edge segments. Both the regions and edge segments are assigned unique positive numbers as labels. The edge segments cannot overlap. The full 2-D problem description can contain several nonintersecting regions, and they can have common border segments. The boundary of a region can consist of several edge segments. All edge segment junctions must coincide with edge segment endpoints. We sometimes refer to an edge segment as a boundary segment or a border segment. A boundary segment is located on the outer boundary of the union of the minimal regions, and a border segment is located on the border between minimal regions.

There are two options for specifying the problem geometry:

• Create a Decomposed Geometry matrix with the function decsg. This is done automatically from pdetool. Using the Decomposed Geometry matrix restricts the edge segments to be straight lines, circle, or ellipse segments. The Decomposed Geometry matrix can be used instead of the Geometry M-file in the toolbox.
• Create a Geometry M-file. By creating your own Geometry M-file, you can create a geometry that follows any mathematical function exactly. Below is an example of how to create a cardioid.

ne=pdegeom is the number of edge segments.

d=pdegeom(bs) is a matrix with one column for each edge segment specified in bs.

• Row 1 contains the start parameter value.
• Row 2 contains the end parameter value.
• Row 3 contains the label of the left-hand region (left with respect to direction induced by start and end from row 1 and 2).
• Row 4 contains the label of the right-hand region.

The complement of the union of all regions is assigned the region number 0.

[x,y]=pdegeom(bs,s) produces coordinates of edge segment points. bs specifies the edge segments and s the corresponding parameter values. bs can be a scalar. The parameter s should be approximately proportional to the curve length. All minimal regions should have at least two, and preferably three, edge segments in their boundary.

Examples

The function cardg defines the geometry of a cardioid

r = 2(1+cos()).

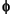• function [x,y]=cardg(bs,s) 
  %CARDG Geometry File defining the geometry of a cardioid. 
  nbs=4; 
  
  if nargin==0  
    x=nbs;   
    return 
  end
  dl=[  0      pi/2   pi       3*pi/2
        pi/2   pi     3*pi/2   2*pi;
        1      1      1        1
        0      0      0        0];
  
  if nargin==1   
    x=dl(:,bs);   
    return 
  end 
  
  x=zeros(size(s)); 
  y=zeros(size(s)); 
  [m,n]=size(bs); 
  if m==1 & n==1,   
    bs=bs*ones(size(s)); % expand bs 
  elseif m~=size(s,1) | n~=size(s,2),   
    error('bs must be scalar or of same size as s'); 
  end 
  
  nth=400; 
  th=linspace(0,2*pi,nth); 
  r=2*(1+cos(th)); 
  xt=r.*cos(th); 
  yt=r.*sin(th); 
  th=pdearcl(th,[xt;yt],s,0,2*pi); 
  r=2*(1+cos(th)); 
  x(:)=r.*cos(th); 
  y(:)=r.*sin(th); 
  

We use the function pdearcl to make the parameter s proportional to arc length. You can test the function by typing

• pdegplot('cardg'), axis equal 
  [p,e,t]=initmesh('cardg'); 
  pdemesh(p,e,t), axis equal
  

Then solve the PDE problem 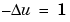on the geometry defined by the cardioid. Use Dirichlet boundary conditions u = 0 on 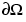. Finally plot the solution.

• u=assempde('cardb',p,e,t,1,0,1); 
  pdesurf(p,t,u); 
  

Cautionary

The parameter s should be approximately proportional to the curve length. All minimal regions should have at least two, and preferably three, edge segments in their boundary.

See Also

initmesh, refinemesh, pdearcl

pdeent

pdegplot