| Partial Differential Equation Toolbox | |
Syntax
Description
The Boundary M-file specifies the boundary conditions of a PDE problem.
The most general form of boundary conditions that we can handle is
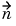· (c 
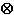
u) +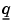 
u = g + h´µ
By the notation 
·(c 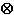u) we mean the N-by-1 matrix with (i,1)-component
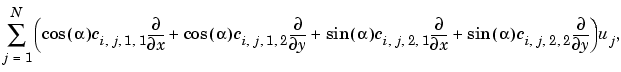
where the outward normal vector of the boundary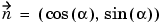 
. There are M Dirichlet conditions and the h-matrix is M-by-N, M 
0. The generalized Neumann condition contains a source h´m where the Lagrange multipliers µ is computed such that the Dirichlet conditions become satisfied.
The data that you specify is q, g, h, and r.
For M = 0 we say that we have a generalized Neumann boundary condition, for M = N a Dirichlet boundary condition, and for 0 < M < N a mixed boundary condition.
The Boundary M-file [q,g,h,r]=pdebound(p,e,u,time) computes the values of q, g, h, and r, on the a set of edges e.
The matrices p and e are mesh data. e needs only to be a subset of the edges in the mesh. Details on the mesh data representation can be found in the entry on initmesh.
The input arguments u and time are used for the nonlinear solver and time stepping algorithms, respectively. u and time are empty matrices if the corresponding parameter is not passed to assemb. If time is NaN and any of the function q, g, h, and r depends on time, pdebound must return a matrix of correct size, containing NaNs in all positions, in the corresponding output argument. It is not possible to explicitly refer to the time derivative of the solution in the boundary conditions.
The solution u is represented by the solution vector u. Details on the representation can be found in the entry on assempde.
q and g must contain the value of q and g on the midpoint of each boundary. Thus we have size(q)=[N^2 ne], where N is the dimension of the system, and ne the number of edges in e, and size(g)=[N ne]. For the Dirichlet case, the corresponding values must be zeros.
h and r must contain the values of h and r at the first point on each edge followed by the value at the second point on each edge. Thus we have size(h)=[N^2 2*ne], where N is the dimension of the system, and ne the number of edges in e, and size(r)=[N 2*ne]. When M < N, h and r must be padded with N - M rows of zeros.
The elements of the matrices q and h are stored in column-wise ordering in the MATLAB matrices q and h.
Examples
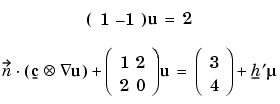
the values below should be stored in q, g, h, and r
1 q=[ ... 2 ... ] 2 0 g=[ ... 3 ... ] 4 1 1 h=[ ... 0 ... 0 ... ] -1 -1 0 0 r=[ ... 2 ... 2 ... ] 0 0
See Also
initmesh, pdegeom, pdesdt, pdeent
| | pdearcl | pdecgrad | |