Block Interleavers (Using the Communications Blockset)

Communications Blockset

Block Interleavers

A block interleaver accepts a set of symbols and rearranges them, without repeating or omitting any of the symbols in the set. The number of symbols in each set is fixed for a given interleaver. The interleaver's operation on a set of symbols is independent of its operation on all other sets of symbols.

Types of Block Interleavers

The set of block interleavers in this library includes a general interleaver/deinterleaver pair as well as several special cases. Each special-case block uses the same computational code that its more general counterpart uses, but provides an interface that is more suitable for the special case.

The Matrix Interleaver block accomplishes block interleaving by filling a matrix with the input symbols row by row and then sending the matrix contents to the output port column by column. For example, if the interleaver uses a 2-by-3 matrix to do its internal computations, then for an input of [1 2 3 4 5 6] the block produces an output of [1 4 2 5 3 6].

The Random Interleaver block chooses a permutation table randomly using the Initial seed parameter that you provide in the block mask. By using the same Initial seed value in the corresponding Random Deinterleaver block, you can restore the permuted symbols to their original ordering.

The Algebraic Interleaver block uses a permutation table that is algebraically derived. It supports Takeshita-Costello interleavers and Welch-Costas interleavers. These interleavers are described in [4].

Example: Block Interleavers

The following example shows how to use an interleaver to improve the error rate when the channel produces bursts of errors.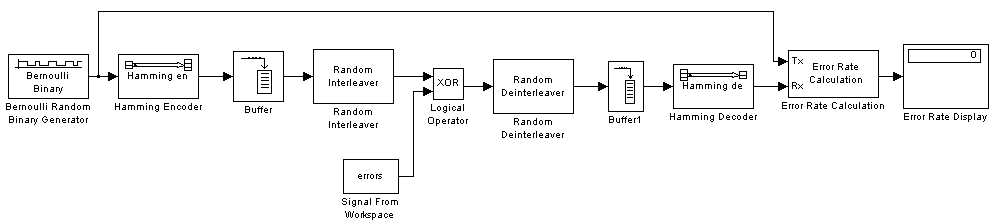

Before running the model, you must create a binary vector that simulates bursts of errors, as described in Creating the Vector of Errors. The Signal From Workspace block imports this vector from the MATLAB workspace into the model, where the Logical Operator block XOR's it with the signal.

To open the completed model, click here in the MATLAB Help browser. To build the model, gather and configure these blocks:

Bernoulli Binary Generator, in the Data Sources sublibrary of the Comm Sources library

Check the box next to Frame-based outputs.

Set Samples per frame to 4.

Hamming Encoder, in the Block sublibrary of the Error Detection and Correction library. Use default parameters.

Buffer, in the Buffers sublibrary of the Signal Management library in the DSP Blockset

Set Output buffer size (per channel) to 84.

Random Interleaver, in the Block sublibrary of the Interleaving library in the Communications Blockset.

Set Number of elements to 84.

Logical Operator, in the Simulink Math Operations library

Set Operator to XOR.

Signal From Workspace, in the DSP Sources library

Set Signal to errors.

Set Sample time to 4/7.

Set Samples per frame to 84.

Random Deinterleaver, the Block sublibrary of the Interleaving library in the Communications Blockset

Set Number of elements to 84.

Buffer, in the Buffers sublibrary of the Signal Management library in the DSP Blockset

Set Output buffer size (per channel) to 7.

Hamming Decoder, in the Block sublibrary of the Error Detection and Correction library. Use default parameters.

Error Rate Calculation, in the Comm Sinks library

Set Receive delay to (4/7)*84.

Set Computation delay to 100.

Set Output data to Port.

Display, in the Simulink Sinks library. Use default parameters.

Select Simulation parameters from the model's Simulation menu and set Stop time to length(errors).

Creating the Vector of Errors

Before running the model, use the following code to create a binary vector in the MATLAB workspace. The model uses this vector to simulate bursts of errors. The vector contains blocks of three 1s, representing bursts of errors, at random intervals. The distance between two consecutive blocks of 1s is a random integer between 1 and 80.

errors=zeros(1,10^4);
n=1;
while n<10^4-80;
n=n+floor(79*rand(1))+3;
errors(n:n+2)=[1 1 1];
end

To determine the ratio of the number of 1s to the total number of symbols in the vector errors, type

```
sum(errors)/length(errors)
```

Your answer should be approximately 3/43, or .0698, since after each sequence of three 1s, the expected distance to the next sequence of 1s is 40. Consequently, you expect to see three 1s in 43 terms of the sequence. If there were no error correction in the model, the bit error rate would be approximately .0698.

When you run a simulation with the model, the error rate is approximately .019, which shows the improvement due to error correction and interleaving. You can see the effect of interleaving by deleting the Random Interleaver and Random Deinterleaver blocks from the model, connecting the lines, and running another simulation. The bit error rate is higher without interleaving because the Hamming code can only correct one error in each code word.

Interleaving Convolutional Interleavers