Communications Blockset

Convolutional Interleavers

A convolutional interleaver consists of a set of shift registers, each with a fixed delay. In a typical convolutional interleaver, the delays are nonnegative integer multiples of a fixed integer (although a general multiplexed interleaver allows arbitrary delay values). Each new symbol from the input signal feeds into the next shift register and the oldest symbol in that register becomes part of the output signal. The schematic below depicts the structure of a convolutional interleaver by showing the set of shift registers and their delay values D(1), D(2),..., D(N). The blocks in this library have mask parameters that indicate the delay for each shift register. The delay is measured in samples.

This section discusses

• The types of convolutional interleavers included in the library
• The delay between the original sequence and the restored sequence
• An example that uses a convolutional interleaver

Types of Convolutional Interleavers

The set of convolutional interleavers in this library includes a general interleaver/deinterleaver pair as well as several special cases. Each special-case block uses the same computational code that its more general counterpart uses, but provides an interface that is more suitable for the special case.

The most general block in this library is the General Multiplexed Interleaver block, which allows arbitrary delay values for the set of shift registers. To implement the preceding schematic using this block, you would use an Interleaver delay parameter of [D(1); D(2); ...; D(N)].

More specific is the Convolutional Interleaver block, in which the delay value for the kth shift register is (k-1) times the block's Register length step parameter. The number of shift registers in this block is the value of the Rows of shift registers parameter.

Finally, the Helical Interleaver block supports a special case of convolutional interleaving that fills an array with symbols in a helical fashion and empties the array row by row. To configure this interleaver, use the Number of columns of helical array parameter to set the width of the array, and use the Group size and Helical array step size parameters to determine how symbols are placed in the array. See the reference page for the Helical Interleaver block for more details and an example.

Delays of Convolutional Interleavers

After a sequence of symbols passes through a convolutional interleaver and a corresponding convolutional deinterleaver, the restored sequence lags behind the original sequence. The delay, measured in symbols, between the original and restored sequences is

(Number of shift registers) * (Maximum delay among all shift registers)

for the most general multiplexed interleaver. If your model incurs an additional delay between the interleaver output and the deinterleaver input, then the restored sequence lags behind the original sequence by the sum of the additional delay and the amount in the preceding formula.

Note    For proper synchronization, the delay in your model between the interleaver output and the deinterleaver input must be an integer multiple of the number of shift registers. You can use the Integer Delay block in the DSP Blockset to adjust delays manually, if necessary.

Convolutional Interleaver block.   In the special case implemented by the Convolutional Interleaver/Convolutional Deinterleaver pair, note that the number of shift registers is the Rows of shift registers parameter, while the maximum delay among all shift registers is

(Register length step)*(Rows of shift registers-1)

Helical Interleaver block.   In the special case implemented by the Helical Interleaver/Helical Deinterleaver pair, the delay between the restored sequence and the original sequence is

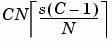
where C is the Number of columns in helical array parameter, N is the Group size parameter, and s is the Helical array step size parameter.

Example: Convolutional Interleavers

The example below illustrates convolutional interleaving and deinterleaving using a sequence of consecutive integers. It also illustrates the inherent delay and the effect of the interleaving blocks' initial conditions.

To open the completed model, click here in the MATLAB Help browser. To build the model, gather and configure these blocks:

• Ramp, in the Simulink Sources library. Use default parameters.
• Zero-Order Hold, in the Simulink Discrete library. Use default parameters.
• Convolutional Interleaver
• Set Rows of shift registers to 3
• Set Initial conditions to [-1 -2 -3]'.
• Convolutional Deinterleaver
• Set Rows of shift registers to 3.
• Set Initial conditions to [-1 -2 -3]'.
• Two copies of To Workspace, in the Simulink Sinks library
• Set Variable name to interleaved and restored, respectively, in the two copies of this block.
• Set Save format to Array in each of the two copies of this block.

Connect the blocks as shown in the preceding diagram. Also, from the model window's Simulation menu, choose Simulation parameters; then, in the Simulation Parameters dialog box, set Stop time to 20. Run the simulation, then execute the following command.

• comparison = [[0:20]', interleaved, restored]
  
  comparison =
  
       0     0    -1
       1    -2    -2
       2    -3    -3
       3     3    -1
       4    -2    -2
       5    -3    -3
       6     6    -1
       7     1    -2
       8    -3    -3
       9     9    -1
      10     4    -2
      11    -3    -3
      12    12     0
      13     7     1
      14     2     2
      15    15     3
      16    10     4
      17     5     5
      18    18     6
      19    13     7
      20     8     8
  

In this output, the first column contains the original symbol sequence. The second column contains the interleaved sequence, while the third column contains the restored sequence.

The negative numbers in the interleaved and restored sequences come from the interleaving blocks' initial conditions, not from the original data. The first of the original symbols appears in the restored sequence only after a delay of 12 symbols. The delay of the interleaver-deinterleaver combination is the product of the number of shift registers (3) and the maximum delay among all shift registers (4).

Block Interleavers

Selected Bibliography for Interleaving