gfmul (Communications Toolbox)

Multiply elements of a Galois field

Syntax

c = gfmul(a,b,p);
c = gfmul(a,b,field);

Description

Note This function performs computations in GF(p^m) where p is odd. To work in GF(2^m), apply the .* operator to Galois arrays. For details, see Example: Multiplication.

The gfmul function multiplies elements of a Galois field. (To multiply polynomials over a Galois field, use gfconv instead.)

c = gfmul(a,b,p) multiplies a and b in GF(p). Each entry of a and b is between 0 and p-1. p is a prime number. If a and b are matrices of the same size, then the function treats each element independently.

c = gfmul(a,b,field) multiplies a and b in GF(p^m), where p is a prime number and m is a positive integer. a and b represent elements of GF(p^m) in exponential format relative to some primitive element of GF(p^m). field is the matrix listing all elements of GF(p^m), arranged relative to the same primitive element. c is the exponential format of the product, relative to the same primitive element. See Representing Elements of Galois Fields for an explanation of these formats. If a and b are matrices of the same size, then the function treats each element independently.

Examples

Arithmetic in Galois Fields contains examples. Also, the code below shows that 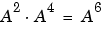, where A is a root of the primitive polynomial 2 + 2x + x² for GF(9).

p = 3; m = 2;
prim_poly = [2 2 1];
field = gftuple([-1:p^m-2]',prim_poly,p);
a = gfmul(2,4,field)

a =

     6

See Also
gfdiv, gfdeconv, gfadd, gfsub, gftuple

gfminpol gfpretty