Communications Toolbox

gfadd

Add polynomials over a Galois field

Syntax

• c = gfadd(a,b,p);
  c = gfadd(a,b,p,len);
  c = gfadd(a,b,field);
  

Description

Note    This function performs computations in GF(pm) where p is odd. To work in GF(2m), apply the + operator to Galois arrays of equal size. For details, see Example: Addition and Subtraction.

c = gfadd(a,b,p) adds two GF(p) polynomials, where p is a prime number. a, b, and c are row vectors that give the coefficients of the corresponding polynomials in order of ascending powers. Each coefficient is between 0 and p-1. If a and b are matrices of the same size, then the function treats each row independently.

c = gfadd(a,b,p,len) adds row vectors a and b as in the previous syntax, except that it returns a row vector of length len. The output c is a truncated or extended representation of the sum. If the row vector corresponding to the sum has fewer than len entries (including zeros), then extra zeros are added at the end; if it has more than len entries, then entries from the end are removed.

c = gfadd(a,b,field) adds two GF(p^m) elements, where m is a positive integer. a and b are the exponential format of the two elements, relative to some primitive element of GF(p^m). field is the matrix listing all elements of GF(p^m), arranged relative to the same primitive element. c is the exponential format of the sum, relative to the same primitive element. See Representing Elements of Galois Fields for an explanation of these formats. If a and b are matrices of the same size, then the function treats each element independently.

Examples

In the code below, sum5 is the sum of 2 + 3x + x² and 4 + 2x + 3x² over GF(5), and linpart is the degree-one part of sum5.

• sum5 = gfadd([2 3 1],[4 2 3],5)
  
  sum5 =
  
       1     0     4
  
  linpart = gfadd([2 3 1],[4 2 3],5,2)
  
  linpart =
  
       1     0
  

The code below shows that 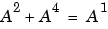, where A is a root of the primitive polynomial 2 + 2x + x² for GF(9).

• p = 3; m = 2;
  prim_poly = [2 2 1];
  field = gftuple([-1:p^m-2]',prim_poly,p);
  g = gfadd(2,4,field)
  
  g =
  
       1
  

Other examples are in Arithmetic in Galois Fields.

See Also
gfsub, gfconv, gfmul, gfdeconv, gfdiv, gftuple

gf

gfconv