Communications Toolbox

gfminpol

Find the minimal polynomial of an element of a Galois field

Syntax

• pol = gfminpol(k,m,p);
  pol = gfminpol(k,prim_poly,p);
  

Description

Note    This function performs computations in GF(pm) where p is odd. To work in GF(2m), use the minpol function with Galois arrays. For details, see Minimal Polynomials.

pol = gfminpol(k,m,p) finds the minimal polynomial of 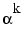over GF(p), where p is a prime number, m is an integer greater than 1, and 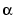is a root of the default primitive polynomial for GF(p^m). The format of the output is as follows:

• If k is a nonnegative integer, then pol is a row vector that gives the coefficients of the minimal polynomial in order of ascending powers.
• If k is a vector of length len all of whose entries are nonnegative integers, then pol is a matrix having len rows; the rth row of pol gives the coefficients of the minimal polynomial of 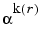in order of ascending powers.

pol = gfminpol(k,prim_poly,p) is the same as the first syntax listed, except that 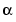is a root of the primitive polynomial for GF(p^m) specified by prim_poly. prim_poly is a row vector that gives the coefficients of the degree-m primitive polynomial in order of ascending powers.

Examples

The syntax gfminpol(k,m,p) is used in the sample code in Characterization of Polynomials.

See Also
gfprimdf, gfcosets, gfroots

gflineq

gfmul