Communications Toolbox

gfdeconv

Divide polynomials over a Galois field

Syntax

• [quot,remd] = gfdeconv(b,a,p);
  [quot,remd] = gfdeconv(b,a,field);
  

Description

Note    This function performs computations in GF(pm) where p is odd. To work in GF(2m), use the deconv function with Galois arrays. For details, see Multiplication and Division of Polynomials.

The gfdeconv function divides polynomials over a Galois field. (To divide elements of a Galois field, use gfdiv instead.) Algebraically, dividing polynomials over a Galois field is equivalent to deconvolving vectors containing the polynomials' coefficients, where the deconvolution operation uses arithmetic over the same Galois field.

[quot,remd] = gfdeconv(b,a,p) divides the polynomial b by the polynomial a over GF(p) and returns the quotient in quot and the remainder in remd. p is a prime number. b, a, quot, and remd are row vectors that give the coefficients of the corresponding polynomials in order of ascending powers. Each coefficient is between 0 and p-1.

[quot,remd] = gfdeconv(b,a,field) divides the polynomial b by the polynomial a over GF(p^m) and returns the quotient in quot and the remainder in remd. Here p is a prime number and m is a positive integer. b, a, quot, and remd are row vectors that list the exponential formats of the coefficients of the corresponding polynomials, in order of ascending powers. The exponential format is relative to some primitive element of GF(p^m). field is the matrix listing all elements of GF(p^m), arranged relative to the same primitive element. See Representing Elements of Galois Fields for an explanation of these formats.

Examples

The code below shows that

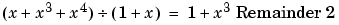
in GF(3). It also checks the results of the division.

• p = 3; 
  b = [0 1 0 1 1]; a = [1 1];
  [quot, remd] = gfdeconv(b,a,p)
  % Check the result.
  bnew = gfadd(gfconv(quot,a,p),remd,p);
  if isequal(bnew,b)
     disp('Correct.')
  end;
  

The output is below.

• quot =
  
       1     0     0     1
  
  
  remd =
  
       2
  
  Correct.
  

Working over GF(3), the code below outputs those polynomials of the form x^k - 1 (k = 2, 3, 4,..., 8) that 1 + x² divides evenly.

• p = 3; m = 2;
  a = [1 0 1]; % 1+x^2
  for ii = 2:p^m-1
     b = gfrepcov(ii); % x^ii
     b(1) = p-1; % -1+x^ii
     [quot, remd] = gfdeconv(b,a,p);
     % Display -1+x^ii if a divides it evenly.
     if remd==0 
        gfpretty(b)
     end
  end
  

The output is below.

•                                          4
                                      2 + X 
   
                                           8
                                      2 + X 
  

In light of the discussion in Algorithm on the reference page for gfprimck along with the irreducibility of 1 + x² over GF(3), this output indicates that 1 + x² is not primitive for GF(9).

Algorithm

The algorithm of gfdeconv is similar to that of the MATLAB function deconv.

See Also
gfconv, gfadd, gfsub, gfdiv, gftuple

gfcosets

gfdiv