gfconv (Communications Toolbox)

Multiply polynomials over a Galois field

Syntax

c = gfconv(a,b,p);
c = gfconv(a,b,field);

Description

Note This function performs computations in GF(p^m) where p is odd. To work in GF(2^m), use the conv function with Galois arrays. For details, see Multiplication and Division of Polynomials.

The gfconv function multiplies polynomials over a Galois field. (To multiply elements of a Galois field, use gfmul instead.) Algebraically, multiplying polynomials over a Galois field is equivalent to convolving vectors containing the polynomials' coefficients, where the convolution operation uses arithmetic over the same Galois field.

c = gfconv(a,b,p) multiplies two GF(p) polynomials, where p is a prime number. a, b, and c are row vectors that give the coefficients of the corresponding polynomials in order of ascending powers. Each coefficient is between 0 and p-1.

c = gfconv(a,b,field) multiplies two GF(p^m) polynomials, where p is a prime number and m is a positive integer. a, b, and c are row vectors that list the exponential formats of the coefficients of the corresponding polynomials, in order of ascending powers. The exponential format is relative to some primitive element of GF(p^m). field is the matrix listing all elements of GF(p^m), arranged relative to the same primitive element. See Representing Elements of Galois Fields for an explanation of these formats.

Examples

The command below shows that

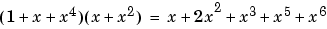over GF(3).

gfc = gfconv([1 1 0 0 1],[0 1 1],3)

gfc =

     0     1     2     1     0     1     1

The code below illustrates the identity

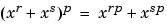in GF(p)

for the case in which p = 7, r = 5, and s = 3. (The identity holds when p is any prime number, and r and s are positive integers.)

p = 7; r = 5; s = 3;
a = gfrepcov([r s]); % x^r + x^s

% Compute a^p over GF(p).
c = 1;
for ii = 1:p
   c = gfconv(c,a,p);
end;

% Check whether c = x^(rp) + x^(sp).
powers = [];
for ii = 1:length(c)
   if c(ii)~=0
      powers = [powers, ii];
   end;
end;
if (powers==[r*p+1 s*p+1] | powers==[s*p+1 r*p+1])
   disp('The identity is proved for this case of r, s, and p.')
end

See Also
gfdeconv, gfadd, gfsub, gfmul, gftuple

gfadd gfcosets