gftuple (Communications Toolbox)

Simplify or convert the format of elements of a Galois field

Syntax

tp = gftuple(a,m,p);
tp = gftuple(a,prim_poly,p);
tp = gftuple(a,prim_poly,p,prim_ck);
[tp,expform] = gftuple(...);

Description

Note This function performs computations in GF(p^m) where p is odd. To perform equivalent computations in GF(2^m), apply the .^ operator and the log function to Galois arrays. For more information, see Example: Exponentiation and Example: Elementwise Logarithm, respectively.

For All Syntaxes

gftuple serves to simplify the polynomial or exponential format of Galois field elements, or to convert from one format to another. For an explanation of the formats that gftuple uses, see Representing Elements of Galois Fields.

In this discussion, the format of an element of GF(p^m) is called "simplest" if all exponents of the primitive element are

Between 0 and m-1 for the polynomial format
Either -Inf, or between 0 and p^m-2, for the exponential format

For all syntaxes, a is a matrix, each row of which represents an element of a Galois field. The format of a determines how MATLAB interprets it:

If a is a column of integers, then MATLAB interprets each row as an exponential format of an element. Negative integers are equivalent to -Inf in that they all represent the zero element of the field.
If a has more than one column, then MATLAB interprets each row as a polynomial format of an element. (Each entry of a must be an integer between 0 and p-1.)

The exponential or polynomial formats mentioned above are all relative to a primitive element specified by the second input argument. The second argument is described below.

For Specific Syntaxes

tp = gftuple(a,m,p) returns the simplest polynomial format of the elements that a represents, where the kth row of tp corresponds to the kth row of a. The formats are relative to a root of the default primitive polynomial for GF(p^m). m is a positive integer and p is a prime number. If possible, the default primitive polynomial is used to simplify the polynomial formats.

tp = gftuple(a,prim_poly,p) returns the simplest polynomial format of the element that a represents, where the kth row of tp corresponds to the kth row of a. p is a prime number. The formats are relative to a root of the primitive polynomial whose coefficients are given, in order of ascending powers, by the row vector prim_poly. If possible, the function uses this primitive polynomial to simplify the polynomial formats.

tp = gftuple(a,prim_poly,p,prim_ck) is the same as tp = gftuple(a,prim_poly,p) except that gftuple checks whether prim_poly represents a polynomial that is indeed primitive. If not, then gftuple generates an error and tp is not returned. The input argument prim_ck can be any number or string; only its existence matters.

[tp,expform] = gftuple(...) returns the additional matrix expform. The kth row of expform is the simplest exponential format of the element that the kth row of a represents. All other features are as described in earlier parts of this "Description" section, depending on the input arguments.

Examples

Some examples are in these subsections of Appendix: Galois Fields of Odd Characteristic:

List of All Elements of a Galois Field (end of section)
Converting to Simplest Polynomial Format
Converting to Simplest Exponential Format

As another example, the gftuple command below generates a list of elements of GF(p^m), arranged relative to a root of the default primitive polynomial. Some functions in this toolbox use such a list as an input argument.

p = 5; % Or any prime number
m = 4; % Or any positive integer
field = gftuple([-1:p^m-2]',m,p);

Finally, the two commands below illustrate the influence of the shape of the input matrix. In the first command, a column vector is treated as a sequence of elements expressed in exponential format. In the second command, a row vector is treated as a single element expressed in polynomial format.

tp1 = gftuple([0; 1],3,3)

tp1 =

     1     0     0
     0     1     0

tp2 = gftuple([0, 0, 0, 1],3,3)

tp2 =


     2     1     0

The outputs reflect that, according to the default primitive polynomial for GF(3³), the relations below are true.

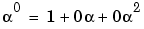
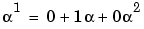
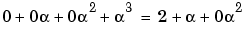
Algorithm

gftuple uses recursive callbacks to determine the exponential format.

See Also
gfadd, gfmul, gfconv, gfdiv, gfdeconv, gfprimdf

gftrunc gfweight