

| Control System Toolbox関数リファレンス |   |
表示
norm(sys) norm(sys,2) norm(sys,inf) norm(sys,inf,tol) [ninf,fpeak] = norm(sys)
詳細
norm
は、連続系または離散系LTIモデルの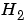 または
または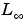 ノルムを計算します。
ノルムを計算します。
H2 ノルム
伝達関数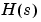 をもつ安定した連続系システムの
をもつ安定した連続系システムの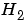 ノルムは、そのImpulse応答の二乗平均の平方根で、つぎの式と等価です。
ノルムは、そのImpulse応答の二乗平均の平方根で、つぎの式と等価です。
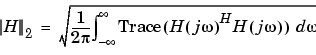
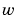 に対する出力応答
に対する出力応答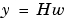 の定常状態共分散(またはベキ乗)になります。
の定常状態共分散(またはベキ乗)になります。
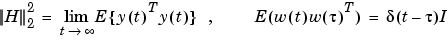
無限大ノルム
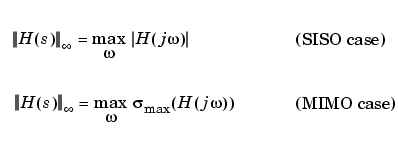
離散系における周波数応答のピークゲインは、つぎのとおりです。
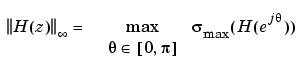
使用方法
norm(sys) 、または、 norm(sys,2)は、TF、SS、ZPKモデルsysの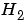 ノルムを出力します。このノルムは、つぎの場合、無限大になります。
ノルムを出力します。このノルムは、つぎの場合、無限大になります。
sysが不安定 sysが連続的で、非ゼロのフィードスルー(すなわち、周波数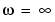 で非ゼロゲイン)をもつ
で非ゼロゲイン)をもつ sqrt(trace(covar(sys,1)))
と同じ結果を生じることに注意してください。norm(sys,inf) は、任意のタイプのLTIモデルsysの無限大ノルムを計算します。このノルムは、sysが連続系で虚軸上、または、離散系で単位円上に極をもつ場合、無限大となります。
norm(sys,inf,tol) は、計算した無限大ノルム上で希望する相対精度を設定します(デフォルト値は、tol=1e-2です)。
[ninf,fpeak] = norm(sys,inf) は、ゲインがそのピーク値に達する周波数fpeakも出力します。
例題
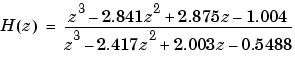
この関数のサンプル時間は0.1秒です。その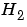 ノルムを、つぎのように計算します。
ノルムを、つぎのように計算します。
H = tf([1 -2.841 2.875 -1.004],[1 -2.417 2.003 -0.5488],0.1) norm(H)MATLABは、つぎの出力を行います。
[ninf,fpeak] = norm(H,inf)MATLABは、つぎの出力を行います。
bode(H)
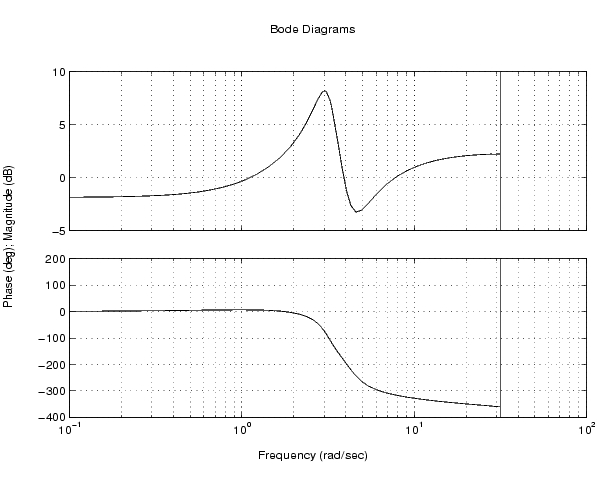
ゲインは、実際、約3ラジアン/秒でピークに達し、dB単位のそのピーク値は、つぎのようになります。
20*log10(ninf)
ans =
8.1268
アルゴリズム
normは、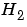 ノルムに対しては、
ノルムに対しては、covarと同じアルゴリズムを使用し、無限大ノルムに対しては、[1]のアルゴリズムを使用します。sysは、まず状態空間型に変換されます。
参考
bode
freqresp
sigma
参考文献
[1] Bruisma, N.A. and M. Steinbuch, "A Fast アルゴリズム to Compute the 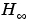 -Norm of a Transfer Function Matrix," System Control Letters, 14 (1990), pp. 287-293.
-Norm of a Transfer Function Matrix," System Control Letters, 14 (1990), pp. 287-293.
 | nichols | nyquist |  |