

| MATLAB Function Reference |   |
表示
T = viewmtx(az,el) T = viewmtx(az,el,phi) T = viewmtx(az,el,phi,xc)
詳細
viewmtx
は、2次元の曲面(たとえば、コンピュータのスクリーン)上に、4次元の同次ベクトルを射影する 4行4列の正射影行列、または、透視投影変換行列を計算します。
T = viewmtx(az,el)
は、方位角 az と仰角 el に対応する正射影変換行列を出力します。azは、視点の方位角(水平方向の回転)を角度で表わしたものです。elは、視点の仰角を角度で表わしたものです。これは、つぎのコマンドの結果と同じ行列を出力します。
view(az,el)
T = view
T = viewmtx(az,el,phi)
は、透視投影変換行列を出力します。phi は、透視法の視点を角度で表わしたものです。phi は、正規化されたプロット立方体の視点角度で、透視法の歪みの量を制御します。
| Phi |
詳細 |
| 0 度 |
正射影 |
| 10 度 |
望遠レンズに似ています |
| 25 度 |
標準レンズに似ています |
| 60 度 |
広角レンズに似ています |
出力される行列を使って、view(T) で視点変換を設定することができます。4行4列の透視投影変換行列は、4次元の同次ベクトルを (x,y,z,w) 形式の正規化されていないベクトルに変換します。ここで、w は、1 ではありません。正規化されたベクトル(x/w, y/w, z/w, 1)の x 成分と y 成分は、希望する 2次元の成分となります(下記の例題を参照)。
T = viewmtx(az,el,phi,xc)
は、正規化されたプロット立方体内部のターゲット点として、xc を使って透視投影変換行列を出力します(つまり、カメラは点 xc で見ています)。xc は、視点の中心にあるターゲット点です。この点は、3 要素ベクトル xc = [xc,yc,zc]で、区間 [0,1] で指定します。デフォルト値は、xc = [0,0,0] です。
注意
4 次元の同次ベクトルは、対応する 3 次元ベクトルに 1 を付け加えたものです。たとえば、[x,y,z,1] は、3 次元の点 [x,y,z] に対応する 4 次元ベクトルです。
例題
デフォルトの視点方向を使って、3 次元の点 (0.5, 0.0, -3.0) に対応する射影された 2 次元ベクトルを決定します。この点は、列ベクトルです。
A = viewmtx(--37.5,30); x4d = [.5 0 --3 1]'; x2d =A*x4d; x2d = x2d(1:2) x2d = 0.3967 --2.4459
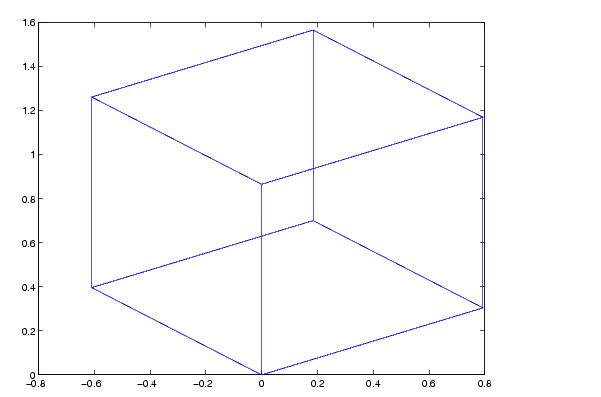
x = [0 1 1 0 0 0 1 1 0 0 1 1 1 1 0 0]; y = [0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 1]; z = [0 0 0 0 0 1 1 1 1 1 1 0 0 1 1 0];
で、これらのベクトル内の点をスクリーンに変換し、オブジェクトをプロットします。
A = viewmtx(--37.5,30); [m,n] = size(x); x4d = [x(:),y(:),z(:),ones(m*n,1)]'; x2d = A*x4d; x2 = zeros(m,n); y2 = zeros(m,n); x2(:) = x2d(1,:); y2(:) = x2d(2,:); plot(x2,y2)
A = viewmtx(--37.5,30,25);
x4d = [.5 0 --3 1]';
x2d = A*x4d;
x2d = x2d(1:2)/x2d(4) % Normalize
x2d =
0.1777
--1.8858
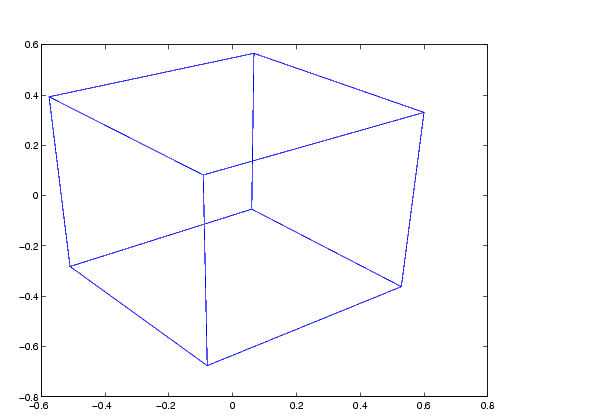
立方体ベクトルをスクリーンに変換し、オブジェクトをプロットします。
A = viewmtx(--37.5,30,25); [m,n] =size(x); x4d = [x(:),y(:),z(:),ones(m*n,1)]'; x2d = A*x4d; x2 =zeros(m,n); y2 = zeros(m,n); x2(:) = x2d(1,:)./x2d(4,:); y2(:) = x2d(2,:)./x2d(4,:);plot(x2,y2)
参考
 | view | volumebounds |  |