

| MATLAB Function Reference |   |
表示
[T,Y] = solver(odefun,tspan,y0) [T,Y] = solver(odefun,tspan,y0,options) [T,Y] = solver(odefun,tspan,y0,options,p1,p2...) [T,Y,TE,YE,IE] = solver(odefun,tspan,y0,options)
ここで、solver は、ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb のいずれかです。
引数
|
微分方程式の右辺を計算する関数。すべてのソルバは、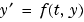 の型の方程式、または、質量行列 の型の方程式、または、質量行列 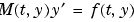 を含む問題のいずれかを解くことができます。 を含む問題のいずれかを解くことができます。ode23s のみは、定質量行列をもつ方程式を解くことができます。ode15s と ode23t は、正則でない質量行列をもつ方程式、すなわち、微分代数方程式を解くことができます。 |
tspan |
積分区間[t0 tfinal] を指定するベクトル。特定の時間(単純増加または単純減少)で解を得るためには、tspan = [t0,t1,...,tfinal]を使います。
|
y0 |
初期条件ベクトル |
|
関数odesetを使って、作成されるオプションの積分引数。odeset を参照してください。 |
p1,p2... |
odefun に渡されるオプションのパラメータ |
詳細
[T,Y] = は、solver(odefun,tspan,y0)
tspan = [t0 tf] のとき、初期状態y0で、t0からtfinalまで微分方程式システム 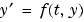 を積分します。スカラ
を積分します。スカラ t 、列ベクトル y に対して、関数 f = odefun(t,y) は、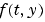 に対応する列ベクトル
に対応する列ベクトル f を出力します。解の配列 Y の各行は、列ベクトル T に出力される時間に対応します。時間 t0, t1,...,tf (単調増加、または、単調減少)での解を求めるためには、tspan = [t0,t1,...,tf] を使ってください。
[T,Y] = は、solver(odefun,tspan,y0,options)
optionsは、関数odesetで作成された引数です(詳細は、 odeset を参照してください)。一般的に使用されるプロパティは、スカラの相対許容誤差RelTol(デフォルトでは、1e-3)と、絶対許容誤差AbsTol(デフォルトでは、1e-6)のベクトルを含みます。
[T,Y] = は、M-ファイルsolver(odefun,tspan,y0,options,p1,p2...)
Fがコールされたときに、付加パラメータp1,p2,...を関数 odefun に渡して、上記のように解きます。オプションを指定しない場合は、options = [] を使ってください。
[T,Y,TE,YE,IE] = は、イベント関数をコールして、関数 solver(odefun,tspan,y0,options)
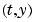 が、ゼロになる位置を見つけながら、上記のように解きます。各イベント関数に対して、ユーザは、積分が、ゼロで終了しているか、そして、ゼロクロスが生じる方向を決めるかを指定することができます。これは、
が、ゼロになる位置を見つけながら、上記のように解きます。各イベント関数に対して、ユーザは、積分が、ゼロで終了しているか、そして、ゼロクロスが生じる方向を決めるかを指定することができます。これは、Events プロパティを @EVENTS に設定し、関数 [value,isterminal,direction] = EVENTS(t,y) を作成することで、処理されます。i 番目のイベント関数に対して、
value(i) は、関数値です。isterminal(i) = 1 に、その他の場合 0 になります。direction(i) = 0、イベント関数が増加する部分でのみゼロになる場合 +1、減少する部分でのみゼロになる場合 -1 になります。TE, YE, IE の中の対応する要素は、各々、イベントが発生した時刻、イベント時刻での解、ゼロになるイベント関数のインデックス i を出力します。
OutputFcn プロパティの値として出力関数を設定する場合、ソルバは、各時間ステップの後で、計算された解と共にコールします。4つの出力関数 odeplot, odephas2, odephas3, odeprint が用意されています。ソルバを出力引数を設定しないでコールすると、デフォルトの odeplot がコールされて、解が計算されながら、プロットされます。odephas2 と odephas3 は、2次元、3次元の位相平面プロットをそれぞれ作成します。odeprint は、スクリーン上に解の成分を表示します。デフォルトでは、解のすべての成分は、出力関数に渡され、OutputSel プロパティの値として、インデックスのベクトルを設定することにより、指定した成分のみを渡すこともできます。たとえば、出力引数を設定しないで、ソルバをコールし、OutputSel の値を [1,3] に設定することにより、ソルバは、解を計算しながら、解の成分1と3をプロットします。
ステッフなソルバ ode15s, ode23s, ode23t, ode23tb に対して、ヤコビアン行列 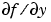 は、信頼性と効率に敏感に影響します。
は、信頼性と効率に敏感に影響します。FJAC(T,Y) が、ヤコビアン 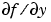 の場合。
の場合。odeset を使って、Jacobian に @FJAC を設定します。または、ヤコビアンが定数の場合は、行列 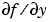 を設定します。
を設定します。Jacobian プロパティが設定されていない(デフォルト)場合、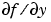 は、有限差分で近似されます。ODE 関数において、
は、有限差分で近似されます。ODE 関数において、odefun(T,[Y1,Y2 ...]) が、[odefun(T,Y1),odefun(T,Y2) ...] を出力するようにコード化されている場合、Vectorized プロパティを 'on' に設定します。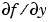 がスパース行列の場合、
がスパース行列の場合、JPattern プロパティを 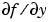 のスパース性パターン、すなわち、
のスパース性パターン、すなわち、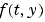 の
の i 番目の要素が、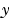 の
の j 番目の要素に依存する場合、S(i,j) = 1 を、その他の場合、S(i,j) = 0 を示すパターンを設定します。
ODE suite のソルバは、時間と状態に依存する質量行列 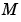 をもつ問題
をもつ問題 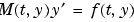 を解くことができます(ソルバ
を解くことができます(ソルバ ode23s は、定質量行列をもつ方程式のみを解くことができます)。問題が質量行列をもつ場合、質量行列の値を出力する関数 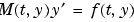 を作成し、
を作成し、odeset を使って、Mass プロパティを @MASS に設定します。質量行列が定数の場合、行列が、Mass プロパティの値として使われます。状態依存の質量行列をもつ問題は、より難しいものになります。
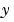 に依存していなく、関数
に依存していなく、関数 MASS が、一入力引数 t と共にコールされる場合、MStateDependence プロパティを 'none' に設定します。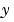 への依存性が弱い場合、
への依存性が弱い場合、MStateDependence を 'weak' (デフォルト) に設定し、他の場合は、'strong' に設定してください。どちらの場合でも、関数
MASS は、2つの引数 (t,y) と共にコールされます。多くの微分方程式が存在する場合、スパース性を利用することは重要です。
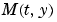 を戻します。
を戻します。 JPattern プロパティを使って、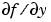 のスパースパターンを与えるか、または、
のスパースパターンを与えるか、または、Jacobian プロパティを使って、スパース 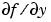 を与えます。
を与えます。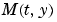 に対して、任意の
に対して、任意の k に対して、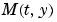 の (
の (i,k) 成分が、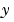 の成分
の成分 j に依存する場合、S(i,j) = 1 で、その他の場合、S(i,j) = 0 であるスパース行列 S を MvPattern に設定します。 質量行列 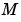 が正則でない場合、
が正則でない場合、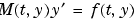 は、微分代数方程式になります。
は、微分代数方程式になります。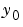 が、無矛盾のときにのみ、
が、無矛盾のときにのみ、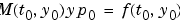 であるベクトルが存在すれば、DAEs は、解をもちます。ソルバ
であるベクトルが存在すれば、DAEs は、解をもちます。ソルバ ode15s と ode23t は、y0 が、無矛盾である状態に十分に近い場合、インデックス1の DAEs を解くことができます。質量行列が存在する場合、関数 odeset を使って、MassSingular プロパティを 'yes', 'no', 'maybe' のいずれかに設定できます。デフォルトは、'maybe' で、問題が、DAE であるか否かのテストを行います。InitialSlope プロパティの初期値として、yp0 を与えることもできます。デフォルトは、ゼロベクトルです。問題が DAE で、y0 と yp0 が、無矛盾の場合、ソルバは、それらを推定値として取り扱い、推定値に近い無矛盾値を計算しようとし、問題を解き続けます。DAEs を解く場合、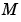 が、対角行列である問題に、定式化できる利点があります。
が、対角行列である問題に、定式化できる利点があります。
ODE ソルバの中で使われるアルゴリズムは、精度の次数 [6] とシステムのタイプ(ステッフ、または、ノンステッフ)に従って、解法を設計します。詳細は、アルゴリズム を参照してください。
オプション
種々のソルバは、オプションリストの中で、種々のパラメータを受け入れます。詳細については、odeset と MATLAB ドキュメントの数学的な解析の微分方程式の ODE ソルバ性能の改良 を参照してください。
例題
例題 1. この例題は、ノンスティッフシステムの例で、外力のない剛体の挙動についての方程式システムです。
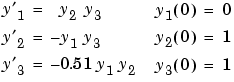
このシステムをシミュレーションするために、つぎの方程式を含むファンクションM-ファイル rigid を作成します。
function dy = rigid(t,y) dy = zeros(3,1); % a column vector dy(1) = y(2) * y(3); dy(2) = -y(1) * y(3); dy(3) = -0.51 * y(1) * y(2);
コマンド odeset で許容誤差を変更し、時間 0での初期条件ベクトル [0 1 1] を用いて、[0 12]の区間で解きます。
options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
[T,Y] = ode45(@rigid,[0 12],[0 1 1],options);
plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.')
例題 2.振動に関するvan der Pol 式によるスティッフなシステムの例です。このリミットサイクルには、解の成分がゆっくりと変化し、問題がスティッフな領域とスティッフでない非常に激しい変化のある領域が交互にあります。
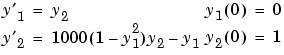
このシステムをシミュレーションするために、つぎの方程式を含むファンクションM-ファイル vdp1000 を作成します。
function dy = vdp1000(t,y) dy = zeros(2,1); % a column vector dy(1) = y(2); dy(2) = 1000*(1 - y(1)^2)*y(2) - y(1);
この問題に対して、デフォルトの相対誤差と絶対誤差(1e-3、1e-6)を使い、時間 0 での初期条件ベクトル [2 0] を用いて、時間区間[0 3000] で解きます。
[T,Y] = ode15s(@vdp1000,[0 3000],[2 0]);
出力行列 Y の最初の列とT をプロットして、解を示します。
plot(T,Y(:,1),'-o'):
アルゴリズム
ode45 は、Dormand-Prince の Runge-Kutta (4,5)の明示的な式に基づいています。これは、y(tn) の計算における1ステップソルバであり、1つ前の時間での解 y(tn-1) のみを必要とします。一般に、ode45はほとんどの問題に対して、最初の試みとして行うのに最も適している関数です[3]。
ode23 は、Bogacki と Shampineによる明示的な Runge-Kutta (2,3) を実現したものです。粗い許容値やわずかなスティッフ性のあるときには、ode45よりも効率的です。ode45 と同様に、ode23は1ステップソルバです[2]。
ode113 は、可変次数のAdams-Bashforth-Moulton PECE ソルバです。厳重な許容値や ODE ファイル関数が特に計算量が多い場合には、ode45よりも効率的です。ode113 は、マルチステップソルバです。カレントの解の計算のために、数ステップ前の時刻での解を通常必要とします[7]。
上記のアルゴリズムは、ノンスティッフなシステムを解くためのものです。これらが過度に遅い場合は、以下のスティッフなソルバのどれかを使ってみてください。
ode15s は、数値微分式(numerical differentiation formulas:NDF) に基づく可変ソルバです。オプションで、NDFよりも効率的でない後退微分式 (backward differentiation formulas(BDF,Gear法としても知られています))を使います。ode113と同様に、ode15sは、マルチステップソルバです。問題が、スティッフである可能性がある場合や、ode45では失敗したり、非常に非効率であった場合は、ode15sを実行してみてください[9], [10]。
ode23s は、2次の修正Rosenbrock式に基づいています。これは、1ステップソルバなので、粗い許容値では、ode15sよりも効率的かもしれません。これは、ode15sでは、効率的でないスティッフな問題を解くことができます[9]。
ode23t は、"フリー"な内挿子を使って、台形則を実行します。問題が、わずかなステッフ性をもち、数値的な減衰が存在しない場合、このソルバを使ってください。 ode23t は、DAEs を解くことができます[10]。
ode23tb は、TR-BDF2の改良版で、最初のステージで、陰的なRunge-Kutta式を使った台形則で、2番目のステップで、2次の後退微分方程式を使います。過程で、同じ繰り返し行列が、2つのステージで計算に使われます。ode23sのように、このソルバは、粗い許容誤差においては、ode15sより、効率的かも知れません[8], [1] 。
参考
@ (function_handle), odeset, odeget
参考文献
Bank, R. E., W. C. Coughran, Jr., W. Fichtner, E. Grosse, D. Rose, and R. Smith, "Transient Simulation of Silicon Devices and Circuits," IEEE Trans. CAD, 4 (1985), pp 436-451.
Bogacki, P. and L. F. Shampine, "A 3(2) pair of Runge-Kutta formulas," Appl. Math. Letters, Vol. 2, 1989, pp 1-9.
Dormand, J. R. and P. J. Prince, "A family of embedded Runge-Kutta formulae," J. Comp. Appl. Math., Vol. 6, 1980, pp 19-26.
Forsythe, G. , M. Malcolm, and C. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, New Jersey, 1977.
Kahaner, D. , C. Moler, and S. Nash, Numerical Methods and Software, Prentice-Hall, New Jersey, 1989.
Shampine, L. F. , Numerical Solution of Ordinary Differential Equations, Chapman & Hall, New York, 1994.
Shampine, L. F. and M. K. Gordon, Computer Solution of Ordinary Differential Equations: the Initial Value Problem, W. H. Freeman, San Francisco, 1975.
Shampine, L. F. and M. E. Hosea, "Analysis and Implementation of TR-BDF2," Applied Numerical Mathematics 20, 1996.
Shampine, L. F. and M. W. Reichelt, "The MATLAB ODE Suite," SIAM Journal on Scientific Computing, Vol. 18, 1997, pp 1-22.
Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, "Solving Index-1 DAEs in MATLAB and Simulink," SIAM Review, Vol. 41, 1999, pp 538-552.
 | nzmax | odefile |  |