

| Mathematics |   |
ODEソルバのデフォルトのプロパティは、一般的な問題を取り扱うために設定されています。ある場合においては、これらのデフォルトを書き換えて、ODE ソルバの性能を改良することができます。これを行うために、引数optionsに含まれる1つまたは複数のプロパティをソルバに設定します。
[t,y] = solver(odefun,tspan,y0,options)
つぎと、それに続くプロパティ表の中で、最も一般的に使われているプロパティが最初にリストされ、より高度なものがそれに続いて表示されています。
| プロパティカテゴリ |
プロパティ名 |
| 誤差のコントロール |
RelTol, AbsTol, NormControl |
| ソルバ出力 |
OutputFcn, OutputSel, Refine, Stats |
| ヤコビアン行列 |
Jacobian, JPattern, Vectorized |
| ステップサイズ |
InitialStep, MaxStep |
| M質量行列と DAE 問題 |
Mass, MStateDependence, MvPattern, MassSingular, InitialSlope |
| イベントの生じる位置 |
Events |
ode15s-specific |
MaxOrder, BDF |
ODE Options 構造体の作成と取り扱い
Options 構造体の作成 関数odesetは、ODE ソルバに引数として渡すことのできるoptions構造体を作成します。odesetは、つぎのような書式で与えたいプロパティの名前とその値とを組にして設定します。
options = odeset('name1',value1,'name2',value2,...)
このようにして、指定された名前のプロパティに特定の値を設定したoptionsを作成します。いくつかの設定されていないプロパティは、ソルバの中ではデフォルトを使います。すべてのプロパティに対して、プロパティ名をユニークに識別できる最初の数文字のみの入力でも構いません。odesetは、プロパティ名として、大文字、小文字の区別を行いません。
入力引数がないとき、odesetは全てのプロパティ名とその取り得る値を示し、設定しているデフォルト値には{ }を付けています。
設定されているoptionsの構成の変更 つぎの書式で、すでに設定されている引数optionsを変更します。
options = odeset(oldopts,'name1',value1,...)
これは、既に存在している構造体oldoptsの値を、プロパティ名/値の組で設定したもので、書き直したり、新しい組を構造体に加えて、構造体optionsを書き換えることができます。出力引数として、書き換えられた構造体が出力されます。同様にして、つぎのコマンド
options = odeset(oldopts,newopts)
では、 oldopts と newopts を組み合わせます。2番目の引数に含まれるプロパティが、最初の引数に含まれるプロパティと一致している場合、2番目の引数に含まれるプロパティで書き換えられて、出力引数に、新しくなったプロパティを含め、構造体全体が出力されます。
Optionsの確認
odeget で設定した options構造体から、あるプロパティの値を取り出すために、関数odesetを使います。
o = odeget(options,'name')
これによって、optionsの中で設定していたプロパティ値を取り出します。設定されていない値に対しては空行列[]が出力されます。
odesetと同様に、プロパティ名はそれを特定できる最初の何文字かの設定で十分で、プロパティ名は、大文字、小文字の区別を行いません。
誤差のコントロールプロパティ
各積分ステップにおいて、ソルバは、解のi番目の要素に、局所的な誤差を計算します。この誤差が、指定した相対許容誤差RelTol、絶対許容誤差AbsTolを比べて、小さいか、等しくなければなりません。
|e(i)|max(RelTol*abs(y(i)),AbsTol(i))
ルーチン問題に対して、ODEソルバは、ユーザが要求した精度におおまかに等しい精度にします。これは、長い区間に渡って積分する問題に対しては、精度を低くしたものを使い、また、不安定な問題についても精度を低くしたものを使います。難しい問題は、デフォルトの値よりも条件の厳しい許容範囲を使うことを必要とします。相対精度に対しては、RelTolを調整します。絶対誤差許容範囲に対しては、解の要素のスケーリングが重要になります。|y| が、AbsTolよりやや小さい場合、ソルバは、yの中の正しい桁数を保証できません。解の要素のスケールを見つけるために、何回か問題を解く必要があります。
おおまかに言って、スレッシュホールドAbsTol(i)より小さいものを除いて、すべての解の要素の中で、RelTolの桁数を必要とすることを意味しています。小さくて、要素y(i)に興味がない場合、y(i)の中にいくつかの正しい桁数を得るのに十分小さなAbsTol(i)を設定する必要があります。それで、興味のある要素を正確に計算することができます。
つぎの表は、誤差のコントロールプロパティを記述しています。odeset を使って、プロパティを設定してください。
つぎのテーブルは、ソルバが生成する出力をコントロールするプロパティをまとめたものです。これらのプロパティを設定するには、odesetを使います。
| プロパティ |
値 |
詳細 | ||
OutputFcn |
関数 {odeplot} |
設定する出力関数。ソルバは、連続的な積分ステップの後で、この関数をコールします。 たとえば、 options = odeset('OutputFcn',@myfun)は、 OutputFcnプロパティを出力関数myfunに設定し、ODEソルバに渡すことができます。出力関数は、つぎの型をしている必要があります。 status = myfun(t,y,flag)ソルバは、つぎのフラグと共に指定した出力関数をコールします。コールする書式は、フラグによって変更することに注意してください。関数は、適切に対応します。 | ||
|
init |
シミュレーションを始める前に、出力関数を初期化するために、ソルバは、myfun(tspan,y0,'init')をコールします。tspanとy0 は、ODE ソルバへの入力引数です。 |
||
|
{none} |
myfunが意図した機能を実行するように、各ステップの後で、ソルバは、status = myfun(t,y) をコールします。t は、区間[a,b] の間の単点で、yは、その点での数値解です。myfunは、0か、1のいずれかからなる statusを出力します。 status = 1の場合、ソルバはシミュレーションを停止します。ユーザは、この機能を使って、Stop ボタンを実行する仕組みを作ることができます。 |
||
|
done |
シミュレーションが終了したとき、クリーンアップをするために、ソルバは、myfun([],[],'done') をコールします。 |
||
|
ユーザは、一般的な目的出力関数を使用でき、または、それをエデットして、ユーザ自身のものを作成できます。 | |||
OutputSel |
インデックスベクトル |
プロパティOutputSelは、解ベクトルのどの要素を出力関数に受け渡すかを特定したインデックスベクトルです。たとえば、出力関数odeplotを使って、1番目と3番目の要素のみをプロットしたいときに、これを使うことができます。options = odeset('OutputFcn',@odeplot,'OutputSel',[1 3]); | ||
Refine |
正の整数 |
出力点数を、Refine倍します。Refineが1の場合、ソルバは、各時間ステップの最後でのみ解を出力します。整数n >1で与えられるプロパティRefine は、出力点の数をn倍に増やして、滑らかな出力を作ります。Refineは、length(tspan)>2の場合、適用されません。
Refine用に作成されるエクストラの値は、連続に拡張した方程式を使って計算されます。これらは、計算時間を極端に増やさないで、計算される時間ステップ間で正確な解を得るために、ODE ソルバで使われる方程式を設定します。 | ||
Stats |
on | {off} |
Statsプロパティで積分計算に関する統計量などの情報について表示するかどうかを設定します。デフォルトでは、Statsはoffです。これが、onの場合、計算終了後、つぎのような項目が表示されます。 | ||
Jacobian行列プロパティ
スティッフなODEソルバは、ユーザがJacobian行列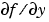 、すなわち微分方程式を定義する関数の偏微分行列についての情報を与えると、実行が速くなります。
、すなわち微分方程式を定義する関数の偏微分行列についての情報を与えると、実行が速くなります。
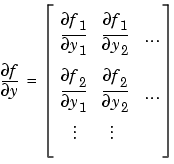
Jacobian 行列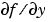 は、信頼性と効率性に敏感なので、ステッフなソルバ(
は、信頼性と効率性に敏感なので、ステッフなソルバ(ode15s, ode23s, ode23t, ode23tb) にのみ、Jacobian 行列プロパティを使います。
Jacobian を計算する関数を与えない場合、これらのステッフなソルバは、有限差分を使って、数値的に Jacobian を近似します。この場合、Vectorized、または、JPattern プロパティを使うこともできます。
つぎのテーブルは、Jacobian 行列プロパティをまとめたもので、詳細も記述しています。これらのプロパティを設定するには、odeset を使ってください。
| プロパティ |
値 |
詳細 |
Jacobian |
関数/定数行列 |
ステッフな問題に対して、解の算出スピードや信頼性の改善のため、Jacobian 関数、または、定数行列を使用します。このプロパティを関数FJacに設定します。ここで、FJac(t,y)は、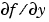 を計算するか、 を計算するか、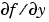 の定数を計算します。 の定数を計算します。上に示したステッフな van der Pol 問題 に対して、Jacobian は、つぎのようにコード化されます。 function J = vdp1000jac(t,y) J = [ 0 1 (-2000 |
JPattern |
{0,1}のスパース行列 |
Jacobianの中で、ゼロでない要素に1をもつスパース行列。これは、数値的なスパースなJacobian 行列を作成するために使われます。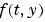 の成分 の成分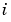 が、 が、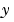 の成分 の成分 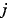 に依存している場合、 に依存している場合、 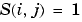 で、他の場合、0であるスパース行列 で、他の場合、0であるスパース行列 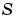 にこのプロパティを設定します。ソルバは、このプロパティを使って、数値的に、スパース Jacobian行列を作成します。Jacobian 行列が大きくて、スパースの場合、実行速度が著しく向上します。Jacobian プロパティを使った例題として、例題 :大規模、ステッフスパース問題( にこのプロパティを設定します。ソルバは、このプロパティを使って、数値的に、スパース Jacobian行列を作成します。Jacobian 行列が大きくて、スパースの場合、実行速度が著しく向上します。Jacobian プロパティを使った例題として、例題 :大規模、ステッフスパース問題(brussode) を参照してください。 |
Vectorized |
on | {off} |
onに設定すると、F(t,[y1 y2 ...]) が、ベクトル[F(t,y1) F(t,y2) ...]を出力するように、ODE 関数 F がコード化されているか否かをステッフソルバに知らせます。
これは、Jacobian 行列のすべての列を計算するのに必要とされる関数計算の回数を減らします。そして、解を計算する時間を実質的に減らすことになります。MATLAB 配列記法を使って、ODE 関数をベクトル化することは、簡単です。たとえば、ステッフな van der Pol の例題は、サブスクリプトにコロン記号 を使い、配列パワー( .^) と配列乗算(.*) を使って、ベクトル化されます。function dydt = vdp1000(t,y) dydt = [y(2,:); 1000*(1-y(1,:).^2).*y(2,:)-y(1,:)]; |
ステップサイズプロパティ
ステップサイズプロパティは、ソルバにより使われる最初のステップサイズを設定し、それを使って問題のスケールを良く認識するのに役に立ちます。それに加え、続いて行なう処理の大きさに範囲を設定できます。
つぎのテーブルは、サテップサイズプロパティをまとめたものです。詳細な説明は、テーブルに従って、その設定については、odesetを使用してください。
| プロパティ |
値 |
詳細 |
InitialStep |
正のスカラ |
初期ステップサイズ。 InitialStepは、ソルバが最初に計算するステップサイズに上限を設定できます。InitialStepを設定していない場合、初期のステップサイズは、初期時間tspan(1)での解の勾配をベースにし、すべての解の要素の勾配がゼロの場合、非常に大き過ぎる値がステップサイズとして利用されることがあります。このような現象が起こることがわかっているときや積分計算を始めるときの重要な振舞いを確実に解きたい場合に適切なInitialStepを設定してください。 |
MaxStep |
正のスカラ値{0.1*abs(t0-tf)} |
このプロパティは、ソルバが使うステップサイズの大きさに上限を設定します。微分方程式が周期性をもつ係数か、または、解をもっている場合、MaxStepを周期の数分の1(例えば1/4倍)に設定することが良い場合があります。これは、ソルバが時間ステップを大きく引き伸ばしたりしなく、対象の区間全体をカバーすることを保証します。
|
質量行列と DAE プロパティ
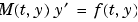
|
(17-2) |
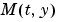 が正則な場合、上の方程式は、
が正則な場合、上の方程式は、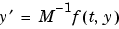 と等価になり、ODEは、
と等価になり、ODEは、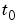 で、任意の初期値
で、任意の初期値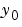 に対する解をもちます。より一般的な型 (式 17-2) は、質量行列の項でモデルを一般的に表現する場合、便利です。大規模な、スパース
に対する解をもちます。より一般的な型 (式 17-2) は、質量行列の項でモデルを一般的に表現する場合、便利です。大規模な、スパース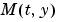 に対して、式 17-2を直接解くことは、ストレージの節約や、必要な実行時間の節約になります。
に対して、式 17-2を直接解くことは、ストレージの節約や、必要な実行時間の節約になります。
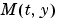 が正則でない場合、
が正則でない場合、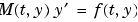 は、微分代数方程式(DAE)になります。DAEは、
は、微分代数方程式(DAE)になります。DAEは、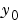 に矛盾がない場合、すなわち、
に矛盾がない場合、すなわち、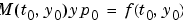 のような初期勾配
のような初期勾配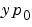 が存在する場合、のみ解をもちます。
が存在する場合、のみ解をもちます。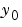 と
と 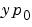 が矛盾する場合、ソルバは、それらを推定として使い、推定に近い矛盾のない値を計算し、問題を解くことを続けます。インデックス1 のDAEs に対して、矛盾のない初期条件をもつ初期値問題を解くことは、ODEを解くことと同じです。
が矛盾する場合、ソルバは、それらを推定として使い、推定に近い矛盾のない値を計算し、問題を解くことを続けます。インデックス1 のDAEs に対して、矛盾のない初期条件をもつ初期値問題を解くことは、ODEを解くことと同じです。
関数ode15s と ode23t は、インデックス1のDAEsを解くことができます。DAE問題の例として、 hb1dae (例題:微分代数問題) と amp1daeを参照してください。
つぎのテーブルは、質量行列とDAE プロパティをまとめたものです。詳細な説明は、テーブルに従ってください。これらのプロパティを設定するには、odeset を使います。
| プロパティ |
値 |
詳細 |
Mass |
定数行列 | 関数 |
質量行列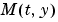 を計算する関数、または、定数質量行列です。
問題 を計算する関数、または、定数質量行列です。
問題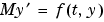 に対して、このプロパティを定数行列の値 に対して、このプロパティを定数行列の値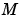 に設定します。
問題 に設定します。
問題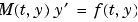 に対して、このプロパティを関数 に対して、このプロパティを関数Mfunへのこのプロパティに設定します。ここで、Mfun(t,y) は、質量行列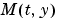 を計算する関数です。 DAEsを解く場合、 を計算する関数です。 DAEsを解く場合、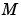 が対角行列(半陽的な DAE)であるように問題を定式化して利用します。関数 が対角行列(半陽的な DAE)であるように問題を定式化して利用します。関数ode23sは、定数質量行列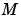 をもつ問題のみを解くことができます。 をもつ問題のみを解くことができます。例題の問題は、 fem1ode (例題:有限要素離散化),fem2ode、または、batonodeを参照してください。 |
MStateDependence |
none | {weak} | strong |
質量行列の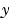 への依存性。問題 への依存性。問題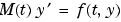 に対して、このプロパティに に対して、このプロパティにnoneを設定します。weakとstrong は共に、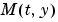 を示しますが、 を示しますが、weak は、代数方程式を解く場合、近時を使って、インプリシットに解きます。 |
MvPattern |
スパース行列 |
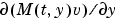 スパース行列。任意の スパース行列。任意の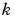 に対して、 に対して、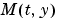 の の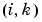 成分が、 成分が、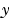 の成分 の成分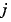 に依存している場合、 に依存している場合、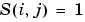 で、他の場合、0をもつスパース行列 で、他の場合、0をもつスパース行列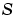 にこのプロパティを設定します。 にこのプロパティを設定します。MStateDependence が、strongの場合、ソルバode15s, ode23t, ode23tbを使います。例題としては、例題:有限要素離散化 (fem1ode)を参照してください。 |
InitialSlope |
ベクトル | {ゼロ ベクトル} |
矛盾のない初期勾配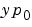 を表すベクトル。ここで、 を表すベクトル。ここで、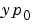 は、 は、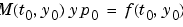 を満足します。デフォルトは、ゼロベクトルです。 を満足します。デフォルトは、ゼロベクトルです。このプロパティは、DAEsを解く場合、関数 ode15s と ode23tと共に使います。 |
イベントの発生個所に関するプロパティ
ODE問題の中で、ボールが地面に達する時刻や宇宙船が地球に帰ってくる時刻、ODEの解がある値に達する時刻等のような特別のイベントの時刻が重要になることがあります。問題を解いている間、MATLABのODEソルバはユーザが定義した関数のベクトルがどこからどこまでゼロになるのか、その移り変わりの場所を求めます。
つぎのテーブルは、Events プロパティに関する説明です。このプロパティを設定するには、odeset を使ってください。
| 文字列 |
値 |
詳細 |
Events |
関数 |
MATLABは、一つ、または、複数のカイベント関数を含んでいます。MATLABは、つぎの型で使います。[ value, isterminal, directionは、ベクトルで、その i番目の要素は、i番目のイベント関数に対応します。
TE、 YE、 IEを戻します。options = odeset(`Events',@events)
[T,Y,TE,YE,IE] =
イベント関数を使った例題について、例題:単純なイベントの発生( |
ode15s のプロパティ
ode15sは、可変次数のスティッフソルバで数値微分公式(NDFs)に基づく手法です。NDFsは、Gear法としても知られている後退微分公式(BDFs)と非常に良く似た手法ですが、より効率的なものです。ode15s のプロパティでは、NDFsかBDFsの選択と公式の最大次数の設定が行えます。
つぎのテーブルは、ode15s プロパティを記述しています。これらのプロパティを設定するには、odeset を使ってください。
| プロパティ |
値 |
詳細 |
MaxOrder |
1 | 2 | 3 | 4 | {5} |
解を計算するために使用する最大次数 |
BDF |
on | {off} |
デフォルトのNDFsの代わりに BDFsを使用する場合に設定。BDF on に設定することは、ode15s に、BDFを使わせることになります。NDFsもBDFsも1または2次では、A-安定です。(安定領域は、複素平面の左半面全てを含みます)これより高い次数は、同様の安定性をもたず、次数が高いほど不安定さが増します。もっとも安定な公式が使われるようにするために、 MaxOrderの値を小さくし(例えば2にする)、より効果的に解くことのできるステイッフな問題(スティッフなときの解の振動)のクラスがあります。 |
 | ODE 問題の表現 | 例題:ODE 初期値問題ソルバの適用 |  |