MATLAB Function Reference

odefile

ODE ソルバに対する微分方程式問題の定義

注意    つぎのリファレンスページは、MATLAB Version 5 で使用されている ODE ソルバのシンタックスと odefile の記述をしています。MATLAB, Version 6 では、前のバージョンの odefile をサポートしていますが、新しいシンタックスは、ODE ファイルを使用しません。新しい機能は、新しいシンタックスでのみ利用可能です。新しいシンタックスに関する情報は、ODE ソルバ、または、odeset を参照してください。

詳細

odefile は、コマンドや関数ではありません。解こうとする方程式のシステムを定義するM-ファイルの作成方法を記述した、ヘルプのエントリです。この定義は、MATLABの ODE ソルバの使用の最初のステップです。MATLABのドキュメントでは、この M-ファイルは、どのような名前を付けても、odefile として参照されます。

つぎの型のいずれかの微分方程式システムを定義するために、odefile を使います。

または、

です。ここで、

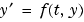
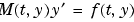
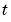• は、スカラの独立変数で、時間を表わします。
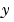• は、従属変数のベクトルです。
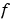• は、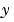 と同じ長さの列ベクトルを戻す 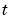と 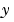の関数です。
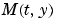• は、時間と状態に依存した質量行列です。

ODEファイルは、使う必要がなくても、引数 t と y を指定しなければなりません。デフォルトでは、ODEファイルは、y と同じ長さの列ベクトルを出力しなければなりません。

ODE suite のすべてのソルバは、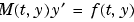 を解くことができます。但し、ode23s は除きます。これは、定質量行列の問題のみに対応しているものです。ode15s と ode23t は、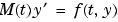 の型をしたいくつかの微分代数方程式(DAEs)を解くことができます。

微分方程式システムの定義では、ODE M-ファイルで完全な初期値問題(IVP) を指定することができ、コマンドラインでの時間と初期値ベクトルの入力を省略できます（例題 を参照)。

ODEファイルのテンプレートの使用法

• コマンド help odefile を入力し、ヘルプのエントリを表示します。
• 別のファイルに、ODEファイルのテキストをカットアンドペーストします。
• ユーザの初期値問題に対して適切でない部分を削除するため、ファイルを編集します。
• 適切な情報を挿入します。ODE システムの定義では、情報が必要とされます。

switch flag
 case ''                      % Return dy/dt = f(t,y).
   varargout{1} = f(t,y,p1,p2);
 case 'init'                 % Return default [tspan,y0,options].
   [varargout{1:3}] = init(p1,p2);
 case 'jacobian'            % Return Jacobian matrix df/dy.
   varargout{1} = jacobian(t,y,p1,p2);
 case 'jpattern'            % Return sparsity pattern matrix S.
   varargout{1} = jpattern(t,y,p1,p2);
 case 'mass'                 % Return mass matrix.
   varargout{1} = mass(t,y,p1,p2);
 case 'events'               % Return [value,isterminal,direction].
   [varargout{1:3}] = events(t,y,p1,p2);
 otherwise
   error(['Unknown flag ''' flag '''.']);
 end
% -------------------------------------------------------------
function dydt = f(t,y,p1,p2)
 dydt = < Insert a function of t and/or y, p1, and p2 here. >
% -------------------------------------------------------------
function [tspan,y0,options] = init(p1,p2)
 tspan = < Insert tspan here. >;
 y0 = < Insert y0 here. >;
 options = < Insert options = odeset(...) or [] here. >;
% ------------------------------------------------------------
function dfdy = jacobian(t,y,p1,p2)
 dfdy = < Insert Jacobian matrix here. >;
% ------------------------------------------------------------
function S = jpattern(t,y,p1,p2)
 S = < Insert Jacobian matrix sparsity pattern here. >;
% ------------------------------------------------------------
function M = mass(t,y,p1,p2)
 M = < Insert mass matrix here. >;
% ------------------------------------------------------------
function [value,isterminal,direction] = events(t,y,p1,p2)
 value = < Insert event function vector here. >
 isterminal = < Insert logical ISTERMINAL vector here.>;
 direction = < Insert DIRECTION vector here.>;

Notes

1. ODE ファイルは、ODE ソルバからベクトル t と y を受け取り、y と同じ長さの列ベクトルを出力しなければなりません。オプションの入力引数 flag は、ODE ファイルにより戻される出力タイプ(質量行列、ヤコビアン等)を決定します。
2. ソルバは、様々な時刻で微分方程式システムを評価するために、ODE ファイルを繰り返し、コールします。これは必要な情報です。ユーザは、解くべき ODE システムを定義しなければなりません。
3. switch ステートメントは、ODE ファイルがソルバに適切な情報を渡すことができるように、必要な出力のタイプを指定します(ステップ 4 - 9 を参照) 。
4. デフォルトの初期条件('init') の case 文では、ODE ファイルは、ソルバに基本情報(時間区間、初期条件、オプション)を出力します。ユーザが、この case 文を省略した場合、コマンドラインですべての基本情報を入力しなければなりません。
5. 'jacobian'の case 文では、ODE ファイルはソルバにヤコビアン行列を出力します。スティッフなソルバ ode15s, ode23s, ode23t や ode23tb の性能を改良したいときに、このcase 文を適用します。
6. 'jpattern' の case 文では、ODE ファイルはソルバにヤコビアンスパースパターン行列を出力します。スティッフなソルバに対して数値的にスパースなヤコビアン行列を作成したいときにのみ、このcase 文を適用します。
7. 'mass' の case文では、ODE ファイルはソルバに質量行列を出力します。つぎのいずれかの型のシステムを解く場合のみ、このcase 文を適用します。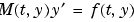
   
8. 'events'の case 文では、ODE ファイルはソルバにイベントの位置選定を行うのに必要な値を出力します。Events プロパティが on に設定されると、ODE ソルバはゼロまで、あるいはゼロから、ゼロを通過する際の変化に対するベクトル event の要素を検証します。論理ベクトル isterminal の対応する要素が 1 に設定されていたら、ゼロとの交差が検出されたときに積分は中止されます。ベクトル direction の要素は、-1, 1, または、0 で、それぞれ対応するイベントが減少、増加、ゼロとの交差が検出されなければならない、ということを指定しています。
9. 認識されない flag は、エラーを生じます。

例題

van der Pol の方程式 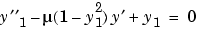は、つぎの連立 1次微分方程式と等価です。

M-ファイル

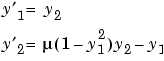
function out1 = vdp1(t,y)
out1 = [y(2); (1-y(1)^2)*y(2) - y(1)]; 

は、この方程式システムを定義します(µ = 1)。

初期値（時間 0 での）が y(1) = 2 で y(2) = 0 のとき、時間区間 [0 20] で van der Pol システムを解くために、つぎのステートメントを使います。

[t,y] = ode45('vdp1',[0 20],[2; 0]); 
plot(t,y(:,1),'-',t,y(:,2),'-.')

M-ファイル内で完全な初期値問題 (IVP) を指定するために、つぎのように vdp1 を書き直します。

function [out1,out2,out3] = vdp1(t,y,flag)
if nargin < 3 | isempty(flag) 
  out1 = [y(1).*(1-y(2).^2)-y(2); y(1)]; 
else
  switch(flag)
    case 'init'               % tspan, y0, and options を戻します。
      out1 = [0 20];
      out2 = [2; 0];
      out3 = [];
  otherwise
    error(['Unknown request ''' flag '''.']);
  end
end

コマンドラインから引数を入力しなくても IVP を解くことができます。

[T,Y] = ode23('vdp1')

この例では、関数 ode23 は省略された引数を与えるために、M-ファイル vdp1 を検証します。一度 optionsを定義するために odeset をコールすると、

[T,Y] = ode23('vdp1',[],[],options)

も実行し、コマンドラインで与えられたoptions は、M-ファイルで指定された対応するオプションを書き換えることに注意してください(odesetを参照)。

参考

MATLAB Version 5 は、ODE ソルバとそれに関連した関数 ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb, odeget, odeset に対するヘルプを用意しています。

MATLAB コマンドラインで、つぎのように入力してください。
more on, type function, more off
Version 5 のヘルプは、Version 6 のヘルプに続きます。

ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb

odeget