griddata (MATLAB Function 参考文献)

データのグリッド化

表示

ZI = griddata(x,y,z,XI,YI)
[XI,YI,ZI] = griddata(x,y,z,xi,yi)
[...] = griddata(...,method)

詳細

ZI = griddata(x,y,z,XI,YI) は、(通常)一様間隔でないベクトル (x,y,z) のデータに、z = f(x,y)型のサーフェスを適合させます。griddata は、ZI を作成するために、(XI,YI)で指定される点で、このサーフェスを補間します。サーフェスは、必ずデータ点を通ります。XIと YIは、通常、一様間隔のグリッドを作成します(meshgridによって、作成されるのと同様です)。

XIは、行ベクトルでも構いません。この場合、列要素が一定の値である行列と考えられます。同様に、YIは、列ベクトルでも構わず、行要素が一定の値である行列と考えられます。

[XI,YI,ZI] = griddata(x,y,z,xi,yi) は、上記のような補間行列 ZI を出力します。また、行ベクトル xiと列ベクトル yi から作成された行列 XI と YI も出力します。これらは、meshgridから出力される行列と同じものです。

[...] = griddata(...,method) は、指定された補間法を使います。

'linear'
三角形ベースの線形補間(デフォルト)

'cubic'
三角形ベースのキュービック補間

'nearest'
最近傍点による補間

'v4'
MATLAB 4 での griddata 法

`'linear'`	三角形ベースの線形補間(デフォルト)
`'cubic'`	三角形ベースのキュービック補間
`'nearest'`	最近傍点による補間
`'v4'`	MATLAB 4 での `griddata` 法

は、データに対するサーフェスの近似タイプを定義します。'cubic'法と 'invdist'法は、滑らかなサーフェスを作成します。一方、'linear' と 'nearest' は、それぞれ、1次導関数と 0次導関数における不連続性をもちます。'invdist'以外のすべての手法は、データの Delaunay三角形分割に基づいています。

注意

XI と YIは、行列でも構いません。この場合、griddata は、対応する点 (XI(i,j),YI(i,j))に対して、値を出力します。また、行ベクトル xi と列ベクトル yi を与えることもできます。この場合、コマンドmeshgrid(xi,yi) によって作成された行列であるかのように、griddataは、これらのベクトルを解釈します。

アルゴリズム

コマンド griddata(...,'v4') は、参考文献[1]の手法を使います。他の手法は、Delaunay三角形分割に基づいています(delaunayを参照)。

例題

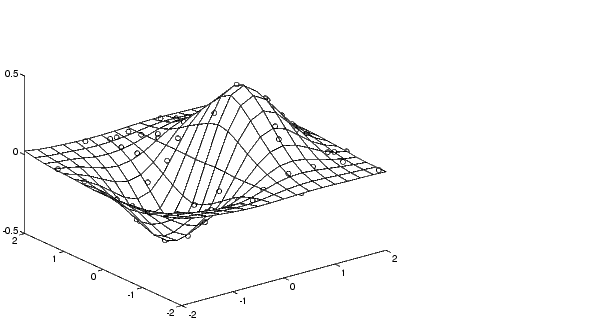
[-2.0 2.0] 内のランダムな 100点で、関数をサンプル化します。

rand('seed',0)
x = rand(100,1)*4-2; y = rand(100,1)*4-2;
z = x.*exp(-x.^2-y.^2);

x, y, and z は、一様間隔でないデータを含んだベクトルです。正規のグリッドを定義し、それを基にグリッドデータを作成します。

ti = -2:.25:2; 
[XI,YI] = meshgrid(ti,ti);
ZI = griddata(x,y,z,XI,YI);

グリッドデータと、それを作成するために使われた一様間隔でないデータをプロットします。

mesh(XI,YI,ZI), hold
plot3(x,y,z,'o'), hold off

参考

delaunay, griddata3, griddatan, interp2, meshgrid

参考文献

[1] Sandwell, David T., "Biharmonic Spline Interpolation of GEOS-3 and SEASAT Altimeter Data", Geophysical Research Letters, 2, 139-142,1987.

[2] Watson, David E., Contouring: A Guide to the Analysis and Display of Spatial Data, Tarrytown, NY: Pergamon (Elsevier Science, Inc.): 1992.

grid griddata3