MATLAB Function Reference

interp2

2次元データ補間(テーブルルックアップ)

表示

ZI = interp2(X,Y,Z,XI,YI)
ZI = interp2(Z,XI,YI)
ZI = interp2(Z,ntimes)
ZI = interp2(X,Y,Z,XI,YI,method)

詳細

ZI = interp2(X,Y,Z,XI,YI) は、XI とYI の要素に対応する要素を含み、X,Y, Z で指定される2次元関数を使って、補間した行列ZI を出力します。X と Y は、単調増加または単調減少で、関数meshgrid で作成されるような同じフォーマット("格子形")をもたなくてはいけません。行列X と Y は、データ Z が与えられる点を指定します。範囲外の値は、NaNとして出力されます。

XI と YI が行列の場合、interp2は、点 (XI(i,j),YI(i,j)) に対応する Zの値を出力します。代わりに、行ベクトルxiや列ベクトルyi として渡すことができます。この場合、interp2は、これらのベクトルをユーザが meshgrid(xi,yi)を実行したかのように解釈します。

ZI = interp2(Z,XI,YI) は、[m,n] = size(Z)に対して、X = 1:n と Y = 1:m であると仮定します。

ZI = interp2(Z,ntimes) は、再帰的に、ntimes回、要素間の補間を繰り返すことにより、Z を拡張します。interp2(Z) は、interp2(Z,1)と同じです。

ZI = interp2(X,Y,Z,XI,YI,method) は、つぎの補間法を指定します。

• 'linear' 線形補間（デフォルト）
• 'nearest' 最近傍点による補間
• 'spline' キュービックスプライン補間
• 'cubic' キュービック補間

すべての補間法で、X と Y は単調関数でなくてはいけません。X と Y は、meshgrid により作成されるものと同じフォーマット("格子形") をもちます。可変間隔の変数は、補間の前に X、Y、XI、YI の値を等間隔の領域に写像して取り扱われます。X と Y が等間隔で、単調増加であるとき、より速い補間を行うために、'*linear'、'*cubic'、'*spline',*nearest' を使ってください。

注意

interp2 は、データ点間の補間を行います。中間点のデータに基づいて、2次元関数 f(x,y) の値を求めます。

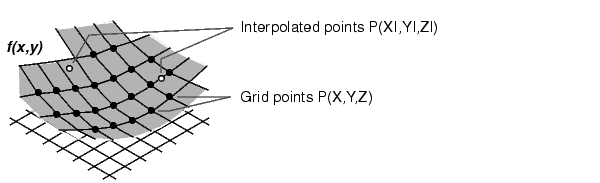
補間は、テーブルルックアップと同じ演算を行います。テーブルルックアップの用語で説明すると、テーブルは tab = [NaN,Y; X,Z] で、interp2は Y の YI 、および、Xの XI の要素を調べ、その位置に基づいて、Zの要素内で補間された値 ZI を出力します。

例題

peaks 関数を細かいグリッド上に補間したの結果をプロットします。

[X,Y] = meshgrid(-3:.25:3);
Z = peaks(X,Y);
[XI,YI] = meshgrid(-3:.125:3);
ZI = interp2(X,Y,Z,XI,YI);
mesh(X,Y,Z), hold, mesh(XI,YI,ZI+15)
hold off
axis([-3 3 -3 3 -5 20])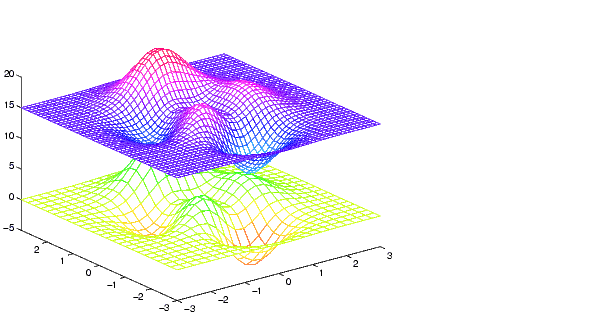

従業員のデータが、以下のように与えられているとします。

years = 1950:10:1990;
service = 10:10:30;
wage = [150.697 199.592 187.625
          179.323 195.072 250.287
          203.212 179.092 322.767
          226.505 153.706 426.730
          249.633 120.281 598.243];

勤続15年の従業員が1975年に得た賃金を、補間することで求められます。

w = interp2(service,years,wage,15,1975)
w =
  190.6287

参考

griddata, interp1, interp3, interpn, meshgrid

interp1

interp3