Mathematics

連立方程式

連立方程式システムは、2つの異なるクラスの方法を使って解かれます。

• 直接法：これは、Gauss消去法を改良し、LUまたはCholesky因子分解のような行列因子分解として表現します。含まれているアルゴリズムは、各々の行列要素にアクセスします。
• 繰り返し法：有限回の繰り返しの後、近似解のみが得られます。係数行列は、行列とベクトルの積を通して、または抜き出した線形演算子の結果として間接的に得られます。

直接法

直接法は、実行するコンピュータが十分なストレージをもっていると、より速く、より一般的に使われるアプローチです。繰り返し法は、制約の付いた方程式に対して使われ、対角部が優勢または微分演算子が存在しているようなプロパティに依存します。直接法は、MATLABのコアの中で実行され、行列の一般的なクラスに対して、できるだけ効果的に機能します。繰り返し法は、通常MATLAB M-ファイルで実現され、サブ問題またはプリコンデション問題に対して直接的に使用します。

MATLABの中で直接法にアクセスする通常の方法は、luまたはcholを使うのではなく、行列除算演算子/または\を使います。Aが正方ならば、X = A\Bは、線形システムA*X = Bの解です。Aが正方でなければ、最小二乗解が計算されます。

Aが、正方で、フルまたはスパース行列ならば、A\Bは、Bと同じストレージクラスをもっています。この計算は、いくつかのアルゴリズムの選択が可能です。

• Aが三角行列ならば、Bの各列に対して三角行列を解きます。
• Aが三角行列の置換ならば、それを置換し、Bの各列に対して、スパース三角行列を解きます。
• Aが対称行列かまたはエルミート行列のどちらかで、正の実数対角要素をもっていると、対称最小次数pを探し、A(p,p)のCholesky因子分解を計算しようとします。うまく行けば、Bの各列に対して、2つのスパース三角行列を解き終了します。
• 他の場合(Aが三角でない、または正の対角要素をもつエルミートでない、またはCholesky分解がうまくできない)、列最小次数pを見つけます。A(:,p)の部分ピポットを使ったLU分解を計算し、Bの各列に対する2つの三角行列を解きます。

正方行列に対して、MATLABはコストの増加のためにこれらの可能性を試します。三角性と対称性のテストは、より速いコンピュータとより多くのメモリ容量を使えるならば、比較的速くなります。

例えば、つぎのステートメント群を考えます。

[L,U] = lu(A);
y = L\b;
x = U\y;

この場合、Lは三角行列の置換で、Uは三角行列なので、MATLABは右、左割り算に対して三角行列を使います。

異なる順序を使って   Aが、三角行列、または、三角行列の置換のどちらでもない場合、バックラッシュ(\) を使って、colmmd と symmmd は、最小次数度合いを決定します。 ユーザが、特定の行列に対して、より良い並びを使いたい場合、関数 spparms を使って、最小次数の前もって与えた並びを切り替えます。

A がスパースで、x = A\b が、LU 因子分解を使っている場合、つぎの例題のように、xに対して解くために、colmmdよりも列の並びを使います。

spparms('autommd',0); 
q = colamd(A);
x = A (:,q) \ b;
x(q) = x;
spparms('autommd',1);

A が、Cholesky 因子分解を使って分解する場合、x = A\b は、つぎのものを使って、効率的に計算されます。

spparms('autommd',0);
p = symamd(A);
x = A(p,p) \ b(p);
x (p) = x;
spparms('autommd',1);

上の例題の中で、ステートメントspparms('autommd',0) は、自動的に、colmmd、または、symmmd 度合いをオフにします。ステートメントspparms('autommd',1) は、元に戻し、ユーザが後で、適切な度合いを設定しないで、使うことができます。引数をもたないで、spparmsを使用すると、スパースパラメータのカレントの設定をレポートします。

繰り返し法

連立線形方程式のスパースシステムを繰り返し法を使って解く9つの関数があります。

関数	詳細
bicg	双共役勾配法
bicgstab	安定化された双共役勾配法
cgs	共役勾配二乗法
gmres	一般化された最小残差法
lsqr	正規方程式での共役勾配のLSQR 実現
minres	最小残差
pcg	Preconditioned共役勾配法
qmr	準最小残差
symmlq	対称 LQ分解

すべての9つの方法が、Ax = bを解くために設計されています。preconditioned共役勾配法pcgは、行列Aが対称で、正定であることが必要です。 minres と symmlq は、対称行列に限られ、行列は、必ずしも正定である必要はありません。lsqrに対して、行列は、正方である必要はありません。 他の5つの関数は、非対称な正方行列を取り扱うことができます。

すべての9つの方法が、左preconditionerと右preconditionerを使います。線形システム

は、つぎの等価な

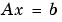
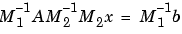
で置き換えます。preconditioner M₁とM₂が、繰り返し法の収束を速めるために選択されます。多くの場合、preconditionerは、数学的なモデルの中で自然に生じます。変数係数をもつ偏微分方程式は、定数係数をもつ偏微分方程式で近似されます。不完全な行列因子分解は、自然のpreconditionerがなくても使うことができます。

正方形上でLaplace方程式に5点の有限差分近似を例題で示します。つぎのステートメントがpreconditionerとして不完全Cholesky因子分解をもつpreconditioned共役勾配法を使います。

A = delsq(numgrid('S',50));
b = ones(size(A,1),1);
tol = 1.e-3;
maxit = 10;
R = cholinc(A,tol);
[x,flag,err,iter,res] = pcg(A,b,tol,maxit,R',R);

たった4回の繰り返しで、前もって設定した精度に達します。

繰り返し法と不完全因子分解に関する背景は、つぎの文献[3] と [7]を参照してください。

因子分解

固有値と特異値