bicg (MATLAB Function 参考文献)

双共役傾斜法

表示

x = bicg(A,b)
bicg(A,b,tol)
bicg(A,b,tol,maxit)
bicg(A,b,tol,maxit,M)
bicg(A,b,tol,maxit,M1,M2)
bicg(A,b,tol,maxit,M1,M2,x0)
bicg(afun,b,tol,maxit,mfun1,mfun2,x0,p1,p2,...)
[x,flag] = bicg(A,b,...)
[x,flag,relres] = bicg(A,b,...)
[x,flag,relres,iter] = bicg(A,b,...)
[x,flag,relres,iter,resvec] = bicg(A,b,...)

詳細

x = bicg(A,b) は、線形方程式A*x = bをxに対して解きます。n行n 列の係数行列 A は、正方である必要があり、列ベクトル b は、長さ n である必要があります。A は、afun(x)が、A*xを出力し、afun(x,'transp')がA'*xを出力する関数afunとすることもできます。

bicg が収束する場合、メッセージとして影響が表示されます。bicg は、設定している繰り返し回数に達しても収束せず、または、何らかの理由で失敗した場合、ワーニングメッセージは、残差norm(b-A*x)/norm(b)と停止した段階での繰り返し回数を示します。

bicg(A,b,tol) は、方法に対するトレランスを設定します。tol を []に設定すると、bicg はデフォルト値1e-6を使います。

bicg(A,b,tol,maxit) は、さらに最大繰り返し回数maxit を指定します。maxit を []に設定すると、bicg はデフォルト値 min(n,20)を使います。

bicg(A,b,tol,maxit,M) と bicg(A,b,tol,maxit,M1,M2) は、左側の前提条件M または、M = M1*M2を使い、inv(M)*A*x = inv(M)*b を xについて、効率的に解きます。M1 または、M2 が空行列 ([])の場合、前提条件は実行されません。M は、mfun(x)がM\x を、mfun(x,'transp')がM'\xを出力する関数mfunにすることができます。

bicg(A,b,tol,maxit,M1,M2,x0) は、初期推定 x0 を指定します。x0が空行列([])の場合、デフォルトの全要素がゼロのベクトルを使います。

bicg(afun,b,tol,maxit,m1fun,m2fun,x0,p1,p2,...) は、パラメータp1,p2,...を関数 afun(x,p1,p2,...) と afun(x,p1,p2,...,'transp') に渡し、前もって設定した関数m1fun と m2fun と同様にします。

[x,flag] = bicg(A,b,...) は、収束フラグも出力します。

フラグFlag
収束

0
bicg は、繰り返し回数 maxit 以内で、希望するトレランスtol 内に収束します。

1
bicg は、繰り返し回数が maxit に達しましたが、収束しませんでした。

2
前提条件子 M の条件数が悪い。

3
bicg は、計算を進めていません(連続する2回の繰り返しの結果が同じでした)。

4
bicgは、関数の中に計算されたスカラ量が、繰り返しを続行するのに小さすぎる、または大きすぎるため、この手法は停止されました。

フラグFlag	収束
`0`	`bicg` は、繰り返し回数 `maxit` 以内で、希望するトレランス`tol` 内に収束します。
`1`	`bicg` は、繰り返し回数が `maxit` に達しましたが、収束しませんでした。
`2`	前提条件子 `M` の条件数が悪い。
`3`	`bicg` は、計算を進めていません(連続する2回の繰り返しの結果が同じでした)。
`4`	`bicg`は、関数の中に計算されたスカラ量が、繰り返しを続行するのに小さすぎる、または大きすぎるため、この手法は停止されました。

flag が 0でないとき、出力された解 x は、すべての繰り返しで計算された中で最小のノルム残差をもつ解です。flagの出力が指定されている場合は、メッセージは表示されません。

[x,flag,relres] = bicg(A,b,...) は、相対残差norm(b-A*x)/norm(b)も出力します。flagが0の場合、relres <= tolになります。

[x,flag,relres,iter] = bicg(A,b,...) は、計算したxでの繰り返し回数も出力します。ここで、0 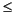iter 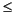maxitです。

[x,flag,relres,iter,resvec] = bicg(A,b,...) は、norm(b-A*x0)を含み、各繰り返しでの残差ノルムのベクトルも出力します。

例題

例題 1

n = 100; 
on = ones(n,1); 
A = spdiags([-2*on 4*on -on],-1:1,n,n);
b = sum(A,2); 
tol = 1e-8; 
maxit = 15;
M1 = spdiags([on/(-2) on],-1:0,n,n); 
M2 = spdiags([4*on -on],0:1,n,n);

x = bicg(A,b,tol,maxit,M1,M2,[]);
bicg converged at iteration 9 to a solution with relative 
residual 5.3e-009

また、つぎの行列-ベクトルの積を計算する関数を使います。

function y = afun(x,n,transp_flag)
if (nargin > 2) & strcmp(transp_flag,'transp')
    y = 4 * x;
    y(1:n-1) = y(1:n-1) - 2 * x(2:n);
    y(2:n) = y(2:n) - x(1:n-1);
else
    y = 4 * x;
    y(2:n) = y(2:n) - 2 * x(1:n-1);
    y(1:n-1) = y(1:n-1) - x(2:n);
end

bicgへの入力として、

   x1 = bicg(@afun,b,tol,maxit,M1,M2,[],n);

例題 2 A = west0479 で始め、すべての要素が1のベクトルを真の解にします。

load west0479;
A = west0479;
b = sum(A,2);

A は、あまり大きくないので、バックスラッシュを使って、A*x = bを正確に解くことができます。

x = A \ b;
norm(b-A*x) / norm(b)

ans =
    1.2454e-017

bicgを使って、 A*x = bを解きましょう。

[x,flag,relres,iter,resvec] = bicg(A,b)

flag =
          1
relres =
          1
iter =
          0

flag の値は、デフォルト設定の20回の繰り返しで、収束しなかったことを意味します。iter の値は、手法が非常に悪い状態で行われたので、初期推定値のゼロの値が、それ以降のすべての繰り返しの結果よりも良かったことを示します。relresの値は、relres = norm(b-A*x)/norm(b) = norm(b)/norm(b)= 1 を提供します。下記のプロット semilogy(0:20,resvec/norm(b),'-o')は、前提条件なしの手法がかなり広範囲に振動したことを確認しています。

semilogy(0:20,resvec/norm(b),'-o')
xlabel('iteration number')
ylabel('relative residual')

さて、前提条件子に関して、1e-5のドロップトレランスを使って、不完全LU 分解を行いましょう。

[L1,U1] = luinc(A,1e-5);
Warning: Incomplete upper triangular factor has 1 zero diagonal.
         It cannot be used as a preconditioner for an iterative 
         method.

nnz(A) 
ans =
         1887
nnz(L1) 
ans =
         5562
nnz(U1) 
ans =
         4320

上三角行列 U1 の主対角上のゼロは、U1 が正則でないことを意味します。それを前提条件子として使う場合、つぎのようになります。

[x,flag,relres,iter,resvec] = bicg(A,b,1e-6,20,L1,U1)

flag =
         2
relres =
         1
iter =
         0
resvec =
         7.0557e+005

バックスラッシュを使って、正則でない U1 を含む方程式を解く場合、最初の繰り返しで失敗します。bicg は、他の繰り返しを起こさないで、初期推定値を出力しようとします。

わずかなスパース性しかもたない前提条件子を使って、再度、試してみます。

[L2,U2] = luinc(A,1e-6)

nnz(L2) 
ans =
         6231
nnz(U2) 
ans =
         4559

今度はワーニングメッセージは表示されません。 U2 の主対角のすべてのエントリはゼロではありません。

[x,flag,relres,iter,resvec] = bicg(A,b,1e-15,10,L2,U2)

flag =
         0
relres =
         2.0248e-16
iter =
         8

bicg は、繰り返し回数 8 回で希望する許容誤差に収束します。ドロップトレランス値を小さくすると不完全成分の要素もより多く満たされますが、オリジナルの行列の近似の精度も良くなります。したがって、L と U が真の LU 成分の場合、前提条件付きシステムは、inv(L)*L*U*inv(U)*y = inv(L)*b に近づき、1 回の繰り返しで解により近づくようになります。

つぎのグラフは、前提条件として、6 個の異なる不完全 LU 分解を使って、bicg の進行を示します。グラフの各ラインは、bicgで使われる前提条件のドロップトレランスのラベルが付けられています。

これは不完全成分を作成して解を計算するために要する時間は考えていません。つぎのグラフには、不完全LU 分解のドロップトレランスに対して、前提条件の計算時間、前提条件が計算されてからの繰り返し時間、それらの合計である問題を解く時間の総計をプロットします。分解を行う時間は、要素を満たすに連れてそれほど速く増加しませんが、繰り返しに対する平均時間まで遅くなります。繰り返しの実行は少なくなるので、問題を解く総時間は減少します。west0479は 139行139列のかなり大きな行列なので、前提条件付きの bicg は、バックスラッシュよりも長く時間がかかります。

参考

bicgstab, cgs, gmres, lsqr, luinc, minres, pcg, qmr, symmlq

@ (関数ハンドル), \ (バックシュラッシュ)

参考文献

Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.

beta, betainc, betaln bicgstab