Mathematics

因子分解

この節では、スパース行列に対して4つの重要な因子分解手法を議論します。

• LU、または、三角分解
• Cholesky分解
• QR、直交分解
• 不完全分解

LU分解

Sがスパース行列なら、つぎのステートメントは、3つのスパース行列L, U, Pを出力します。ここで、この行列には、P*S = L*Uの関係があります。

[L,U,P] = lu(S)

luは部分ピポットを使ったGauss消去法で因子を得ます。置換行列Pは、n個の非ゼロ要素のみを含んでいます。密行列と共に、ステートメント[L,U] = lu(S)は、置換された単位下三角行列と上三角行列でそれらの積がSになる行列を出力します。出力引数なしでは、lu(S)は、ピポット情報なしに単一行列として、LとUを出力します。

スパースLU分解は、スパースに対してピポットを行ないませんが、数値的に安定なものに対しては、ピポットを行ないます。実際に、時間とストレージの必要量が非常に異なるときでも、スパース分解(ライン1)とフルの因子分解(ライン2)は、同じL, Uを出力します。

[L,U] = lu(S)                % スパースに対する因子分解
[L,U] = sparse(lu(full(S)))  % フルに対する因子分解

つぎのコマンドを使って、スパース行列の中のピボットをコントロールすることができます。

lu(S,thresh)

ここで、threshは、[0,1]の中のピボットのスレッシュホールドです。ピボット操作は、ある列の中の対角要素が、その列の中の他のサブ対角要素の大きさの thresh 倍よりも小さい場合に生じます。thresh = 0 は、対角ピボット操作を強制します。thresh = 1 はデフォルトです。

MATLABは、因子分解の間にスパースLとU ファクタを保持するために必要なメモリを自動的に割り当てます。MATLABは、必要なメモリを決めたり、より進んだデータ構造を設定するためにシンボリックなLUプリ因子分解を使いません。

並び替えと因子分解   ユーザが、 symrcmやcolmmdから、fill-in状態を低減する良い列置換pを得ているなら、lu(S(:,p))を計算することは、lu(S)を計算するより時間とストレージともに少なくなります。2つの置換は、対称逆Cuthill-McKee並びと対称最小次元順番です。

r = symrcm(B);
m = symamd(B);

つぎに示すようにラインで作成される3つのspyプロットは、これらの3つの異なる番号付けによるBuckyボールの3つの隣接行列を示しています。オリジナルの番号付けの局所的な多角形をベースにした構造は、他のものの中では、はっきりしていません。

spy(B)
spy(B(r,r))
spy(B(m,m))

逆Cuthill-McGee並びrは、バンド幅を狭くして、対角部近傍にすべての非ゼロ要素を集中せさます。最小次元の並びmは、大きなゼロのブロックをもつフラクタルに似た構造を作成します。

BuckyボールのLU分解で生じるfill-inを見るには、スパース単位行列speye(n,n)を使って、Bの対角要素に-3を設定します。

B = B - 3*speye(n,n);

各行の和がゼロなので、この新しいBは正則ではありません。しかし、LU因子分解を計算することはできます。一つの出力引数のみを定義して、コールすると、単一のスパース行列に、luは2つの三角ファクタL,Uを出力します。この行列の中の非ゼロ要素数は、Bに含まれる線形システムを解くために必要な時間とストレージの尺度になります。つぎに、3つの置換に対する非ゼロカウントを示します。

オリジナル	lu(B)	1022
逆 Cuthill-McKee	lu(B(r,r))	968
最小度合い	lu(B(m,m))	636

これは小さな規模の例題ですが、結果は典型的なものです。オリジナルの番号付けの方法は、大部分がfill-inになります。逆Cuthill-McKee法は、バンド内に集中しますが、最初の2つの番号付けとほぼ同じ量になります。最小次数法では、ゼロの数が比較的大きいブロックは消去作業中に保存され、fill-inの量は他の方法に比べ極端に減ります。つぎのspyプロットは、各々の方法の特徴を示しています。

Cholesky因子分解

Sが対称(またはエルミート)、正定、スパース行列ならば、つぎのステートメント

R = chol(S)

は、R'*R = Sを満たす上三角スパース行列 Rを出力します。cholは、スパースに対しては、自動的にピポットを行ないませんが、chol(S(p,p))の使用に対して最小次数を計算し、制限付置換を探します。

Choleskyアルゴリズムは、スパースに対してピポットを使わず、数値的安定に対してピポットを必要としないので、因子分解の最初にすべてのメモリの割り当てと必要なメモリの総量をすぐ計算できます。

QR因子分解

MATLABは、つぎのステートメント

 [Q,R] = qr(S)

でスパース行列Sの完全なQR分解を行ないます。しかし、実際には、現実的なものではありません。直交行列Qは、ゼロ要素の割合が高いとき、うまく実行できないことがあります。より実際的な変更法、いわゆる"Q-less QR分解"として知られている方法が利用可能になります。

スパース行列を入力引数とし、出力引数を共に1個ずつ設定する

R = qr(S)

は、QR分解の上三角部を出力します。行列Rは正規方程式

R'*R = S'*S

に関連した行列に対するCholesky分解を与えます。しかし、S'*Sの計算の中で固有の数値的情報の欠落が避けられます。

同じ行数をもつ2つの入力引数と2つの出力引数を設定すると、

[C,R] = qr(S,B)

は、Bに直交変換を適用し、Qを実際には計算しませんが、C = Q'*BになるCを作成します。

Q-less QR分解は、スパース最小二乗問題

の解を、つぎの2ステップで出力します。

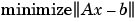
[c,R] = qr(A,b)
x = R\c

Aがスパースで正方でなければ、MATLABは、これらのステップをバックスラッシュ演算子を使って解きます。

x = A\b

または、ユーザは自分自身で因子分解を行ない、ランク落ちに関してはRをチェックしてください。

R = qr(A)が計算されたとき、必ずしも必要ありませんが、異なる右辺bをもつ最小二乗線形連立方程式を解くこともできます。アプローチは、"準正規方程式"

R'*R*x = A'*b

を解きます。ここで、

x = R\(R'\(A'*b))

そして、丸め誤差を低減するために繰り返し計算を行ないます。

r = b - A*x
e = R\(R'\(A'*r))
x = x + e

不完全因子分解

関数luincとcholincは、近似的な、不完全因子分解を与えます。これは、スパース繰り返し法で前置条件として利用可能なものです。

関数luincは、2つの異なる不完全LU因子分解を作成します。1つは、drop toleranceを含んでいるもので、他はfill-inレベルを含んでいるものです。Aがスパース行列で、tolが小さなトレランスのとき、

[L,U] = luinc(A,tol)

は、tolと対象の列のノルムとの乗算値よりも小さなすべての要素をゼロに設定する近似的なLU因子分解を計算します。また、

[L,U] = luinc(A,'0')

は、近似的なLU因子分解を計算します。ここで、L+Uのスパースパターンは、Aのスパースパターンの置換です。

例えば、

load west0479
A = west0479;
nnz(A)
nnz(lu(A))
nnz(luinc(A,1e-6))
nnz(luinc(A,'0'))

は、Aが1887個の非ゼロ要素をもち、この完全なLU因子分解は16777非ゼロをもち、drop toleranceが1e-6を使った不完全LU因子分解は10311個の非ゼロ要素をち、lu('0')因子分解は、1886個の非ゼロ要素をもっています。

関数luincは、2,3のオプションをもっています。詳細は、オンラインヘルプを参照してください。

関数cholincは、drop toleranceと対称、正定スパース行列のlevel 0 fill-in Cholesky分解を作成します。詳細は、オンラインヘルプを参照してください。

置換と並べ替え

連立方程式