MATLAB Function Reference

cgs

共役傾斜二乗法

表示

x = cgs(A,b)
cgs(A,b,tol)
cgs(A,b,tol,maxit)
cgs(A,b,tol,maxit,M)
cgs(A,b,tol,maxit,M1,M2)
cgs(A,b,tol,maxit,M1,M2,x0)
cgs(afun,b,tol,maxit,m1fun,m2fun,x0,p1,p2,...)
[x,flag] = cgs(A,b,...)
[x,flag,relres] = cgs(A,b,...)
[x,flag,relres,iter] = cgs(A,b,...)
[x,flag,relres,iter,resvec] = cgs(A,b,...)

詳細

x = cgs(A,b) は、xに関する線形方程式A*x = bを解きます。n行n列の係数行列 A は、正方で、列ベクトルb は、長さ nである必要があります。A は、afun(x) が、A*xを出力するような関数afunです。

cgs が収束する場合、その影響に関するメッセージが表示されます。cgsが、設定した繰り返し最大回数に達した後や、何らかの理由で、収束しない場合、相対残差 norm(b-A*x)/norm(b)とこの方法が停止した時点での繰り返し回数を表すワーニングメッセージが表示されます。

cgs(A,b,tol) は、この方法で使用できる許容誤差範囲 tolを設定できます。 tolが、[]の場合、cgs は、デフォルト値 1e-6を使います。

cgs(A,b,tol,maxit) は、最大繰り返し回数 maxit　を指定します。maxit が、[] の場合、cgs は、デフォルト min(n,20)　を使います。

cgs(A,b,tol,maxit,M) と cgs(A,b,tol,maxit,M1,M2) は、左側の前提条件M、または、code>M = M1*M2を使い、システムinv(M)*A*x = inv(M)*bを xについて効率良く解きます。M1またはM2が空行列([])ならば、前提条件は適用されません(それらが単位行列であることと等価です)。cgsで、M*y = rの型の方程式をバックスラッシュを使って解くときに、前提条件を最初のLU因子に分解するのが望ましいです。たとえば、cgs(A,b,tol,maxit,M)を、つぎのステートメントで置き換えます。

cgs(A,b,tol,maxit,M1,M2,x0) は、初期推定x0を指定します。x0が空行列([])ならば、デフォルトの全要素がゼロのベクトルが使われます。

cgs(afun,b,tol,maxit,m1fun,m2fun,x0,p1,p2,...) は、パラメータ p1,p2,... を関数 afun(x,p1,p2,...)、m1fun(x,p1,p2,...)、 m2fun(x,p1,p2,...)に渡します。

[x,flag] = cgs(A,b,...) は、解 x とcgsの収束を記述するフラグを表示します。

フラグ	収束
0	code>cgsは、何らかの理由で失敗することなく、繰り返し回数maxit 内で、希望する許容誤差tolに収束しました。
1	cgsは、maxit回の繰り返しを行いましたが、収束しませんでした。
2	前提条件の1つを含むM*y = rの型の方程式システムが条件数が悪くて、\(バックスラッシュ)を実行したときに使用できる結果を得られませんでした。
3	cgsは、計算を進めていません(連続する2回の繰り返しの結果がが同じでした。
4	cgs中に計算されたスカラ量が、繰り返しを続行するのに小さすぎる、または大きすぎるため、この手法は停止されました。

flag が 0でない場合、戻される解 x は、すべての繰り返しを通して計算された最小ノルム残差です。flag 出力が設定されている場合、メッセージは表示されません。

[x,flag,relres] = cgs(A,b,...) also returns the relative residual norm(b-A*x)/norm(b). If flag is 0, then relres 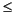tol.

[x,flag,relres,iter] = cgs(A,b,...) also returns the iteration number at which x was computed, where 0 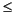 iter 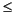maxit.

[x,flag,relres,iter,resvec] = cgs(A,b,...) also returns a vector of the residual norms at each iteration, including norm(b-A*x0).

例題

例題 1.

A = gallery('wilk',21);
b = sum(A,2);
tol = 1e-12;  maxit = 15; 
M1 = diag([10:-1:1 1 1:10]);
x = cgs(A,b,tol,maxit,M1,[],[]);

Alternatively, use this matrix-vector product function

function y = afun(x,n)
y = [ 0; 
      x(1:n-1)] + [((n-1)/2:-1:0)'; 
      (1:(n-1)/2)'] .*x + [x(2:n); 
      0 ];

and this preconditioner backsolve function

function y = mfun(r,n)
y = r ./ [((n-1)/2:-1:1)'; 1; (1:(n-1)/2)'];

as inputs to cgs.

x1 = cgs(@afun,b,tol,maxit,@mfun,[],[],21);

注意 that both afun and mfun must accept cgs's extra input n=21.

例題 2.

load west0479
A = west0479
b = sum(A,2)
[x,flag] = cgs(A,b)

flag is 1 because cgs does not converge to the default tolerance 1e-6 within the default 20 iterations.

[L1,U1] = luinc(A,1e-5)
[x1,flag1] = cgs(A,b,1e-6,20,L1,U1)

flag1 is 2 because the upper triangular U1 has a zero on its diagonal, and cgs fails in the first iteration when it tries to solve a system such as U1*y = r for y with backslash.

[L2,U2] = luinc(A,1e-6)
[x2,flag2,relres2,iter2,resvec2] = cgs(A,b,1e-15,10,L2,U2)

flag2 is 0 because cgs converges to the tolerance of 6.344e-16 (the value of relres2) at the fifth iteration (the value of iter2) when preconditioned by the incomplete LU factorization with a drop tolerance of 1e-6. resvec2(1) = norm(b) and resvec2(6) = norm(b-A*x2). You can follow the progress of cgs by plotting the relative residuals at each iteration starting from the initial estimate (iterate number 0) with

semilogy(0:iter2,resvec2/norm(b),'-o')
xlabel('iteration number')
ylabel('relative residual')

参考

bicg, bicgstab, gmres, lsqr, luinc, minres, pcg, qmr, symmlq

@ (function handle), \ (backslash)

参考文献

Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.

Sonneveld, Peter, "CGS: A fast Lanczos-type solver for nonsymmetric linear systems", SIAM J. Sci. Stat. Comput., January 1989, Vol. 10, No. 1, pp. 36-52.

cellstr

char